Penjelasan Proporsionalitas Komposit, Tiga Aturan Senyawa, Latihan

Itu Komposit atau banyak proporsionalitas Ini adalah hubungan antara lebih dari dua besaran, di mana proporsionalitas langsung dan terbalik dapat diamati antara data dan yang tidak diketahui. Ini adalah versi yang lebih canggih dari proporsionalitas sederhana, meskipun teknik yang digunakan dalam kedua prosedur serupa.

Misalnya, jika 7 orang diperlukan untuk mengunduh 10 ton barang dagangan dalam 3 jam, proporsionalitas majemuk dapat digunakan untuk menghitung berapa banyak orang yang diperlukan untuk mengunduh 15 ton dalam 4 jam.

Sumber: Pixabay.com

Untuk menjawab pertanyaan ini, lebih mudah untuk membuat tabel nilai untuk mempelajari dan menghubungkan besaran dan tidak diketahui.

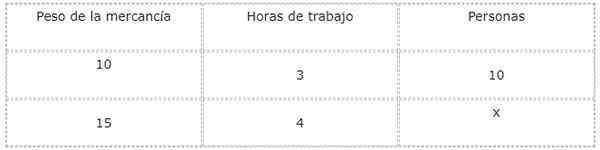
Jenis -jenis hubungan antara setiap besarnya dan yang tidak diketahui saat ini dianalisis, yang dalam hal ini sesuai dengan jumlah orang yang akan bekerja.

Ketika bobot barang dagangan meningkat, jumlah orang yang perlu diunduh juga meningkat. Karena itu, hubungan antara berat badan dan pekerja adalah langsung.

Di sisi lain, dengan meningkatkan jumlah pekerja, jam kerja berkurang. Karena itu, hubungan antara orang dan jam kerja terbalik.

[TOC]

Cara menghitung proporsionalitas senyawa

Untuk memecahkan contoh seperti yang sebelumnya, metode aturan tiga senyawa sebagian besar digunakan. Ini terdiri dalam membangun jenis hubungan antara magnitudo dan tidak diketahui dan kemudian mewakili produk antara pecahan.

Sehubungan dengan contoh awal, fraksi yang sesuai dengan tabel nilai diatur sebagai berikut:

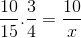
Tetapi sebelum menyelesaikan dan membersihkan, fraksi yang tidak diketahui yang sesuai dengan hubungan terbalik harus dibalik. Bahwa untuk kasus ini sesuai dengan variabel waktu. Dengan cara ini, operasi yang akan diselesaikan adalah:

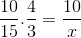
Yang satu -satunya perbedaan adalah investasi fraksi yang sesuai dengan waktu variabel 4/3. Nilai x dioperasikan dan jelas.

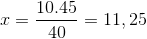
Dengan demikian, lebih dari sebelas orang diperlukan untuk mengunduh 15 ton barang dagangan dalam 4 jam atau kurang.

Penjelasan

Proporsionalitas adalah hubungan konstan antara besaran yang mengalami perubahan, yang akan simetris untuk masing -masing besaran yang terlibat. Ada hubungan proporsional secara langsung dan terbalik, sehingga mendefinisikan parameter proporsionalitas sederhana atau majemuk.

Langsung tiga aturan

Ini terdiri dari rasio proporsi antara variabel, yang menghadirkan perilaku yang sama saat dimodifikasi. Sangat sering dalam perhitungan persentase yang terkait dengan besaran yang berbeda dari seratus, di mana struktur fundamentalnya dihargai.

Sebagai contoh, Anda dapat menghitung 15% dari 63. Pada pandangan pertama, persentase tersebut tidak dapat dilihat dengan cara yang sederhana. Tetapi menerapkan aturan tiga Anda dapat membuat hubungan berikut: jika 100% adalah 63, maka 15%, berapa harganya?

Dapat melayani Anda: Teorema Faktor: Penjelasan, Contoh, Latihan

100%-63

15%-x

Dan operasi yang sesuai adalah:

(limabelas% . 63) / 100% = 9,45

Di mana tanda persentase disederhanakan dan angka 9,45 yang mewakili 15% dari 63 tercapai.

Tiga aturan terbalik

Seperti namanya, dalam hal ini hubungan antara variabel bertentangan. Hubungan terbalik harus ditetapkan sebelum melanjutkan perhitungan. Prosedurnya homolog dengan tiga aturan langsung, dengan pengecualian investasi dalam fraksi yang akan dihitung.

Misalnya, 3 pelukis membutuhkan 5 jam untuk menyelesaikan dinding. Berapa jam 4 pelukis selesai?

Dalam hal ini hubungannya terbalik, karena dengan meningkatkan jumlah pelukis waktu kerja harus berkurang. Hubungan itu ditetapkan;

3 Pelukis - 5 Jam

4 Pelukis- x jam

Saat hubungan terbalik, urutan operasi terbalik. Ini menjadi cara yang benar;

(3 pelukis) . (5 jam) / 4 pelukis = 3,75 jam

Istilah pelukis disederhanakan, dan hasilnya adalah 3,75 jam.

Kondisi

Untuk berada di hadapan senyawa atau proporsionalitas ganda, perlu untuk menemukan kedua jenis hubungan antara besaran dan variabel.

- Langsung: Variabel menyajikan perilaku yang sama dengan yang tidak diketahui. Yaitu, dengan meningkatkan atau mengurangi satu, yang lain diubah secara setara.

- Inverse: Variabel ini menyajikan perilaku antonim dengan yang tidak diketahui. Fraksi yang mendefinisikan variabel ini dalam tabel nilai harus dibalik, untuk mewakili hubungan proporsional terbalik antara variabel dan tidak diketahui.

Verifikasi hasil

Sangat umum untuk membingungkan urutan besarnya ketika bekerja dengan proporsionalitas majemuk, tidak seperti apa yang terjadi dalam perhitungan proporsi yang biasa, yang sifatnya sebagian besar langsung dan resoluble dengan menggunakan aturan tiga sederhana sederhana.

Oleh karena itu, penting untuk memeriksa urutan logis hasil, memverifikasi koherensi angka yang dilemparkan oleh aturan tiga senyawa.

Dalam contoh awal, membuat kesalahan ini akan menyiratkan mendapatkan 20 sebagai hasilnya. Yaitu, 20 orang untuk mengunduh 15 ton barang dagangan dalam 4 jam.

Sekilas, sepertinya bukan hasil yang gila, tetapi peningkatan hampir 200% pada staf (dari 7 menjadi 20 orang) penasaran ketika peningkatan barang dagangan adalah 50%, dan bahkan dengan margin waktu yang lebih besar untuk melakukan bekerja.

Itu dapat melayani Anda: Persamaan Parabola Umum (Contoh dan Latihan)

Dengan cara ini verifikasi logis hasil merupakan langkah penting dengan mengimplementasikan aturan tiga senyawa senyawa.

Izin

Meskipun sifat yang lebih mendasar mengenai pembentukan matematika, izin mewakili langkah penting dalam kasus proporsionalitas. Clearance yang keliru cukup untuk membatalkan hasil apa pun yang diperoleh dalam urutan tiga sederhana atau senyawa.

Sejarah

Aturan tiga diketahui di Barat melalui orang -orang Arab, dengan publikasi oleh beberapa penulis. Di antara mereka al-jwarizmi dan al-biruni.

Al-Biruni, berkat pengetahuan multikulturalnya, memiliki akses ke informasi luas mengenai praktik ini dalam perjalanannya ke India, bertanggung jawab atas dokumentasi paling luas tentang tiga aturan tiga.

Itu meningkatkan penyelidikannya, bahwa India adalah tempat pertama di mana penggunaan tiga aturan dibuat umum. Penulis memastikan bahwa itu dibuat dengan lancar dalam versi langsung, terbalik, dan bahkan disusun.

Tanggal pasti di mana tiga aturan menjadi bagian dari pengetahuan matematika India masih belum diketahui. Namun, dokumen tertua yang ditujukan untuk praktik ini, naskah Bakhshali, ditemukan pada tahun 1881. Saat ini di Oxford.

Banyak sejarawan matematika memastikan bahwa naskah ini berasal dari awal era saat ini.

Latihan terpecahkan

Latihan 1

Maskapai harus memindahkan 1535 orang. Diketahui bahwa dengan 3 pesawat itu akan memakan waktu 12 hari untuk dibawa ke penumpang terakhir ke tujuan. 450 lebih banyak orang telah mencapai maskapai dan 2 pesawat diperintahkan untuk berkolaborasi dengan tugas ini. Berapa hari yang akan dibawa maskapai penerbangan ke penumpang terakhir ke tujuannya?

Hubungan antara jumlah orang dan hari -hari kerja adalah langsung, karena semakin banyak orang, lebih banyak hari akan diperlukan untuk melakukan pekerjaan ini.

Di sisi lain, hubungan antara pesawat terbang dan hari -hari berbanding terbalik. Dengan meningkatkan jumlah pesawat terbang, hari yang diperlukan menurun untuk ditransfer ke semua penumpang.

Tabel nilai yang mengacu pada kasus ini dilakukan.

Sebagaimana dirinci dalam contoh awal, pembilang dan penyebut harus diinvestasikan dalam fraksi yang sesuai dengan variabel terbalik sehubungan dengan yang tidak diketahui. Meninggalkan operasi sebagai berikut:

Dapat melayani Anda: perhitungan pendekatan menggunakan diferensial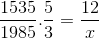

X = 71460/7675 = 9,31 hari

Untuk pindah ke tahun 1985 orang menggunakan 5 pesawat, lebih dari 9 hari diperlukan.

Latihan 2

Panen jagung 25 -ton dibawa ke truk kargo. Diketahui bahwa tahun sebelumnya membutuhkan waktu 8 jam dengan daftar gaji 150 pekerja. Jika untuk tahun ini penggajian meningkat 35%, berapa lama waktu yang dibutuhkan untuk mengisi truk muatan dengan panen 40 -ton?

Sebelum mewakili tabel nilai, jumlah pekerja untuk tahun ini harus ditentukan. Ini meningkatkan 35% dari angka awal 150 pekerja. Untuk ini, aturan tiga langsung digunakan.

100% - 150

35% - x

X = (35 . 100)/100 = 52.5. Ini adalah jumlah pekerja tambahan sehubungan dengan tahun sebelumnya, memperoleh jumlah total 203 pekerja, tidak senang untuk membulatkan jumlah yang diperoleh.

Tabel data yang sesuai didefinisikan

Untuk kasus ini, beratnya mewakili variabel hubungan langsung dengan waktu yang tidak diketahui. Di sisi lain, variabel pekerja mengelola hubungan terbalik dengan waktu. Jumlah pekerja yang lebih besar, hari itu akan lebih singkat.

Dengan mempertimbangkan pertimbangan ini dan menginvestasikan fraksi yang sesuai dengan pekerja, itu dihitung.

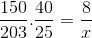
X = 40600 /6000 = 6,76 jam

Hari itu akan memakan waktu kurang dari 7 jam.

Latihan yang diusulkan

- Tentukan 73% dari 2875.

- Hitung jumlah jam yang tidur Teresa, jika diketahui bahwa hanya 7% dari total hari tidur. Tentukan berapa jam tidur dalam seminggu.

- Koran publik 2000 setiap 5 jam, hanya menggunakan 2 mesin cetak. Berapa banyak salinan yang akan diproduksi dalam 1 jam, jika Anda menggunakan 7 mesin? Berapa lama akan menghasilkan 10.000 salinan menggunakan 4 mesin?

Referensi

1. Encyclopedia Alvarez-Iniciacion. KE. Álvarez, Antonio álvarez Pérez. Edaf, 2001.
2. Manual Instruksi Utama Elemental dan Superior: Untuk penggunaan pelamar kepada guru dan terutama siswa sekolah provinsi normal, Volume 1. Joaquín Avendaño. Pencetakan d. Dionisio Hidalgo, 1844.
3. Perkiraan peringkat fungsi nyata. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 Maret. 2011.
4. Aritmatika unsur untuk mengajar di sekolah dan sekolah di Amerika Tengah. Darío González. Tip. Arenales, 1926.
5. Studi Matematika: Pada Studi dan Kesulitan Matematika. Augustus de Morgan. Baldwin dan Cradock, 1830.