Apa angka segitiga? Properti dan demonstrasi

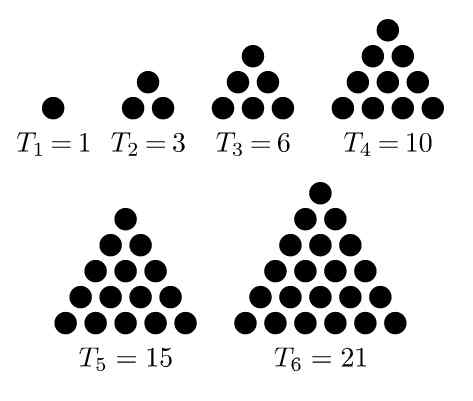
Itu dikenal sebagai angka segitiga ke urutan angka yang diperoleh dengan membuat pengaturan atau angka titik segitiga sama sisi. Urutan pertama adalah: 1, 3, 6, 10, 15, 21, ..

Masalah segitiga pertama adalah 1, yang kedua adalah 3, karena diperoleh dari menambahkan baris dua titik ke yang sebelumnya, untuk membentuk segitiga sama sisi dari tiga elemen.

Gambar 1. Urutan dari enam angka segitiga pertama. Sumber: Wikimedia Commons. Melchoir/CC BY-SA (https: // CreativeCommons.Org/lisensi/by-sa/3.0)

Yang ketiga adalah 6, yang muncul saat menambahkan baris tiga poin ke pengaturan sebelumnya, sehingga segitiga tiga poin terbentuk per sisi. 10 dari urutan diperoleh dengan menambahkan baris lain ke pengaturan sebelumnya sehingga segitiga empat poin terbentuk per sisi.

Rumus yang memungkinkan Anda menemukan elemen N Dari urutan segitiga, diketahui angka segitiga anterior adalah:

T_N = T_N-1 + N

Daftar enam angka segitiga pertama dicapai seperti ini:

-Pertama: 1

-Kedua: 1 + 2 = 3

-Ketiga: (1 +2) + 3 = 3 + 3 = 6

-Ruang: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Kelima: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Keenam: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Sifat bilangan segitiga

1.- Jumlah segitiga N-Simo Tn dari urutan angka segitiga adalah setengah dari N dikalikan dengan n+1:

T_N = ½ N (n+1)

2.- Jumlah bilangan segitiga n-Ésimo dengan angka segitiga anterior, yaitu, (n-1) -sheimo, itu ditinggikan persegi:

T_N + T_N-1= n²

3.- Perbedaan dalam bilangan segitiga n-ini kurang dari n-Ésimo triangular kurang satu adalah n:

T_N - T_N-1 = n

4.- Jumlah angka segitiga pertama disebut angka tetrahedral SN dan sama dengan bagian keenam dari produk dikalikan dengan (n + 1) dan dikalikan dengan (n + 2):

Dapat melayani Anda: pajak

S_N= ⅙ n (n + 1) (n + 2)

5.- Setiap angka alami n adalah hasil dari jumlah tiga angka segitiga:

N = Δ1 + Δ1 + Δ3

Properti atau teorema terakhir ini ditemukan oleh ahli matematika hebat Carl Friedrich Gauss pada 1796, yang ia cetak dalam buku hariannya dengan menempatkan kekaguman Yunani Eureka! apa artinya "Saya telah mencapainya".

Itu adalah kata yang sama yang digunakan jauh lebih awal oleh archimedes Yunani ketika ia menentukan berat badan yang terendam.

Dalam hubungan ini, angka nol dianggap sebagai segitiga dan mungkin ada pengulangan.

Demonstrasi

- Demonstrasi 1

Buktikan bahwa angka segitiga N-Ini:

T_N = ½ N (n+1)

Mudah untuk menyimpulkan formula sebelumnya, jika kita menyadari bahwa kita dapat menambahkan jumlah poin yang sama ke pengaturan segitiga untuk membentuk segi empat poin.

Karena jumlah total titik pengaturan dalam bentuk segi empat adalah jumlah baris N dikalikan dengan jumlah kolom (N+1), Maka pengaturan segitiga hanya akan memiliki setengah dari titik pengaturan dalam bentuk segi empat.

Di sini diilustrasikan pada Gambar 2.

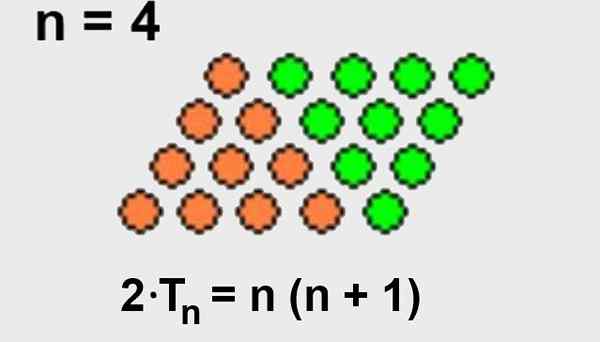Gambar 2. Pengaturan berbentuk kuadrat di mana jumlah total titik adalah jumlah baris n dikalikan dengan jumlah kolom n+1. Jumlah total poin juga dua kali lipat dari pengaturan segitiga. Sumber: Wikimedia Commons.

- Demonstrasi 2

Menunjukkan bahwa jumlah N-Angka segitiga ini dengan N-Kurang satu Angka segitiga adalah N kuadrat:

T_N + T_N-1= n²

Telah ditunjukkan bahwa angka segitiga N-Ini diberikan oleh:

T_N= ½ N (n+1)

Oleh karena itu, angka segitiga anterior adalah:

T_N-1 = ½ (n-1) ((n-1) + 1) = ½ N (n-1)

Jumlah kedua sisa -sisa:

T_N + T_N-1 = ½ N (n + 1) + ½ n (n - 1)

½ N diambil untuk mendapatkan:

T_N + T_N-1 = ½ N [(n + 1) + (n - 1) = ½ N [n + 1 + n - 1]

Dan segera ekspresi disederhanakan di dalam braket:

Itu dapat melayani Anda: estimasi berdasarkan interval

T_N + T_N-1 = ½ n [2 n] = ½ 2 n ⋅ n

Sekarang, mengingat bahwa ½ untuk 2 adalah 1 dan bahwa n untuk n adalah n persegi, Anda memiliki:

T_N + T_N-1 = n²

Properti ini juga dapat ditunjukkan secara geometris, segitiga hanya diselesaikan untuk membentuk kuadrat, seperti yang ditunjukkan pada Gambar 3.

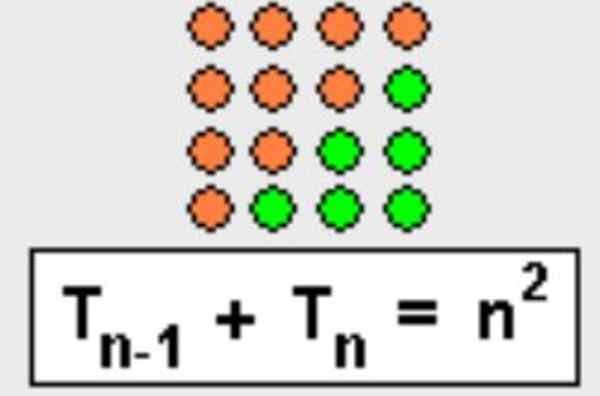Gambar 3. Jumlah nomor segitiga N-Ésimo dengan angka segitiga anterior sama dengan N square. Sumber: Wikimedia Commons.

- Demonstrasi 3

Perbedaan jumlah pesanan segitiga N minus jumlah pesanan segitiga N-1 adalah n:

T_N - T_N-1 = n

Ini dapat diuji hanya dengan mengingat bahwa angka segitiga berikut diperoleh dari yang sebelumnya melalui rumus:

T_N = T_N-1 + N

Dan dari sana jelas itu T_N - T_N-1 = n. Juga mudah untuk memvisualisasikannya secara grafis, seperti yang ditunjukkan pada Gambar 4.

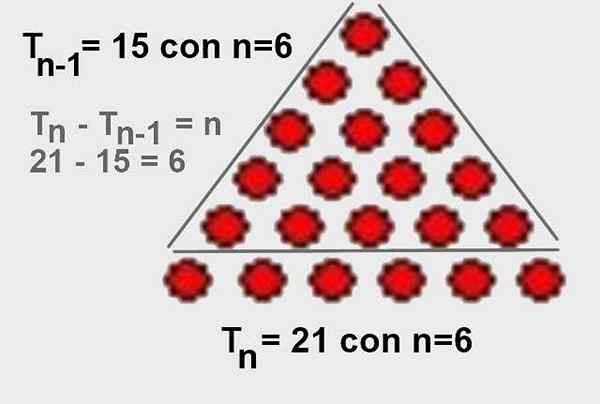Gambar 4. Perbedaan jumlah urutan segitiga dan kurang dari segitiga anterior urutan N-1 adalah n. Sumber: Wikimedia Commons.

- Demonstrasi 5

Jumlah bilangan segitiga pertama sN Ini sama dengan bagian keenam dari produk yang dikalikan dengan (n + 1) dan dikalikan dengan (n + 2):

S_N = ⅙ n (n + 1) (n + 2)

Mari kita gunakan jumlah pesanan segitiga n: T_N= ½ N (n+1). Jumlah yang pertama N Angka segitiga akan menunjukkannya S_N  

Misalnya, S₁ berarti jumlah dari masalah segitiga pertama, yang tidak diragukan lagi akan menjadi 1.

Kemudian mari kita lihat apakah formula yang kami coba coba dipatuhi dengan n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Memang, rumus untuk n = 1 diperiksa. Sangat mudah untuk memvisualisasikan bahwa jumlah angka segitiga pertama N+1 akan menjadi jumlah dari N yang pertama lebih dari angka segitiga berikutnya:

S_N+1 = S_N + T_N+1

Sekarang anggap formula S_N Itu dipenuhi untuk n, lalu kami menggantinya di ekspresi sebelumnya dan menambahkan jumlah pesanan segitiga N+1:

S_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]]

Dapat melayani Anda: garis tegak lurus: karakteristik, contoh, latihan

Mari kita lihat selangkah demi selangkah apa yang diperoleh:

-Kami melaksanakan jumlah dua ekspresi fraksional:

S_N+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Itu dihapus dari pembilang yang umum menjadi 2 (n + 1) (n + 2) dan menyederhanakan:

S_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Hasil sebelumnya setuju dengan formula SN Jika n+1 diganti, yang telah ditunjukkan dengan induksi formula jumlah istilah segitiga pertama.

Nomor tetrahedral

Hasil yang diperoleh dipanggil Jumlah pesanan tetrahedral n, Karena itu seperti mengumpulkan lapisan segitiga yang membentuk tetrahedron, seperti yang ditunjukkan dalam animasi berikut.

Gambar 5. Jumlah angka segitiga N sesuai dengan tumpukan lapisan N, N-1, ..., 1 segitiga yang membentuk tetrahedron biasa. Sumber: Wikimedia Commons.

Referensi

1. Camacho J. Penampilan bilangan segitiga yang tidak disangka -sangka. Pulih dari: Masscience.com
2. Claudio. Angka segitiga. Dipulihkan dari: cukup angka. Blogspot. com
3. Wikipedia. Nomor segitiga. Pulih dari: is.Wikipedia.com
4. Wikipedia. Nomor segitiga. Diperoleh dari: di.Wikipedia.com
5. Wikipedia. Nomor tretrahedral. Diperoleh dari: di.Wikipedia.com