Area dari Pentagon yang biasa dan tidak teratur bagaimana itu diambil, latihan

Untuk menghitung area pentagon Pertama kita perlu menentukan apakah ini biasa atau tidak. Pentagon adalah poligon, sosok datar yang tertutup dari lima sisi. Saat poligon teratur, itu berarti bahwa panjang sisinya sama dan sudut internalnya juga.

Dalam hal ini, ada formula untuk menghitung area yang tepat dari poligon reguler, mengetahui beberapa karakteristik utamanya, yang akan kita sebutkan nanti.

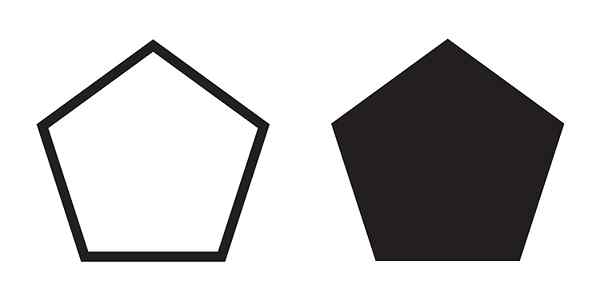Dua pentagon

Jika poligon tidak teratur, yaitu, ia memiliki sisi yang berbeda, dan sudut internal yang tidak setara, tidak ada formula tunggal.

Namun, ahli matematika telah menemukan strategi perhitungan, seperti membagi angka menjadi orang lain dengan jumlah sisi terendah, seperti segitiga, kotak dan persegi panjang, yang dimensinya diketahui atau mudah dihitung.

Prosedur lain untuk menghitung area poligon secara umum, mengetahui koordinat simpulnya, adalah metode yang disebut Penentu Gauss, yang akan kami jelaskan nanti.

[TOC]

Cara menghitung area pentagon biasa?

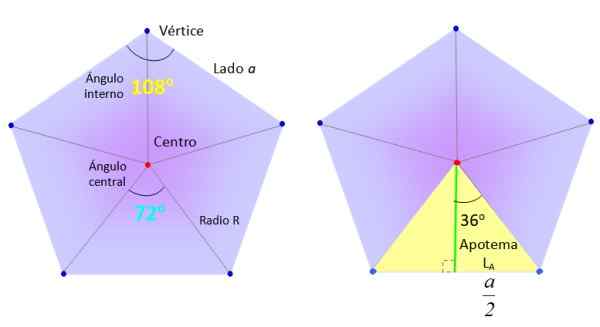
Kami akan mengambil pentagon biasa dari sisi A, dan kami akan membaginya menjadi 5 segitiga yang sama seperti yang ditunjukkan pada gambar, menggambar segmen dari tengah (merah) ke simpul (biru).

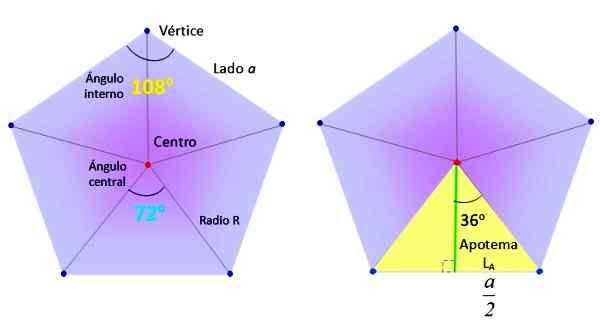Elemen yang diperlukan untuk menemukan area pentagon biasa. Sumber: f. Zapata.

Pada gilirannya, segitiga, seperti kuning yang luar biasa di sebelah kanan pada gambar atas, dibagi menjadi dua persegi panjang yang sama, berkat segmen hijau, yang disebut apothem.

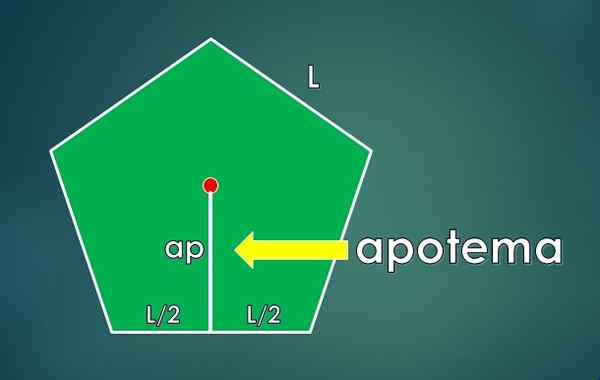
Apotheme didefinisikan sebagai segmen tegak lurus yang terhubung ke pusat poligon dengan pusat satu sisi. Panjangnya adalah l_KE.

Area segitiga persegi panjang dasar A/2 dan tinggi l_KE adalah:

[(A/2) x l_KE]

Pentagon memiliki 10 segitiga seperti ini, oleh karena itu luasnya adalah:

Dapat melayani Anda: fungsi vektor

A = 10 (a/2) x l_KE

Tapi perimeter P Pentagon justru p =10a, Oleh karena itu area tersebut diberikan oleh semi -produk perimeter dan panjang apothem:

A = p x l_KE /2

Area Pentagon biasa mengetahui sisi a

Mengekspresikan panjang apothem l_KE Tergantung pada sisi A, mengetahui bahwa sudut yang ditunjukkan adalah setengah dari sudut tengah, yaitu 36º, setara dengan:

36º = π/5

Oleh trigonometri dasar, dengan singgung sudut akut 36º:

Tan (π/5) = (a/2) ÷ l_KE

Karena itu:

L_KE=  (A/2) ÷ tan (π/5)

Mengganti di area yang dikurangi di bagian sebelumnya, dan mengetahui bahwa p = 5a:

A = p x l_KE /2

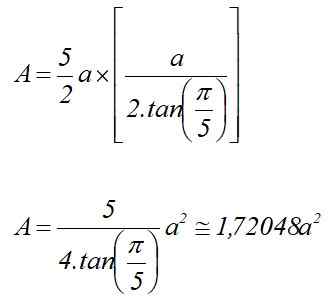
Area Pentagon biasa mengetahui radionya

Dia radio dari poligon biasa adalah segmen yang beralih dari pusat ke salah satu simpulnya. Ini bertepatan dengan jari -jari keliling yang dibatasi, seperti yang ditunjukkan pada gambar berikut:

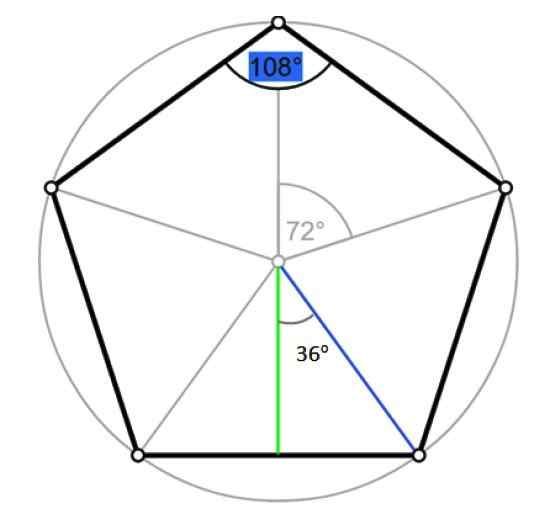Sudut dan apothem dari Pentagon. Sumber: Wikimedia Commons/F. Zapata.

Biarkan R menjadi ukuran radio tersebut, yang bertepatan dengan hypotenuse dari segitiga kanan yang digambarkan pada gambar sebelumnya, dengan warna biru. Dengan trigonometri:

cos 36º = cos (π/5) = l_KE ÷ r

DAN

sin 36º = sin (π/5) = (a/2) ÷ r

Karena itu:

A = p x l_KE /2 = 5r. sin (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]

Menggunakan rumus sudut ganda:

sin (2θ) = 2 sen θ . cos θ

Kita harus:

[sin (π/5) x cos (π/5)] = (1/2) sin 72º

Maka, dengan penggantian nilai ini, kami mendapatkan formula berikut untuk area Pentagon biasa:

A = (5/2) r².Sen 72º

Cara menghitung area pentagon yang tidak teratur?

Seperti yang telah kami katakan sebelumnya, untuk poligon yang tidak teratur tidak ada formula tunggal, tetapi ada dua metode yang biasanya bekerja dengan sangat baik, yang pertama disebut triangulasi dan yang kedua adalah metode penentu Gauss.

Dapat melayani Anda: Teorema Keberadaan dan Keunikan: Demonstrasi, Contoh dan Latihan

Triangulasi

Terdiri dari membagi angka menjadi segitiga, yang luasnya lebih mudah dihitung, atau juga dapat diuji dengan tokoh -tokoh lain yang areanya diketahui, seperti kotak, persegi panjang dan trapesies.

Penentu Gauss

Cara lain untuk menemukan area Pentagon yang tidak teratur atau poligon tidak beraturan lainnya adalah menempatkan sosok itu dalam sistem koordinat Cartesian, untuk menemukan koordinat simpul.

Diketahui koordinat ini, metode penentu Gauss diterapkan untuk menghitung area, yang diberikan oleh rumus berikut:

Di mana A adalah luas poligon dan (x_N , Dan_N ) adalah koordinat simpul. Poligon sisi N memiliki 5 simpul, untuk Pentagon akan menjadi n = 5:

Batang yang menyertai formula adalah batang modul atau nilai absolut.

Ini berarti bahwa meskipun hasil operasi negatif, kita harus mengekspresikannya dengan tanda positif, dan jika sudah positif, itu harus dibiarkan dengan tanda itu. Ini karena suatu area selalu merupakan jumlah yang positif.

Prosedur ini disebut penentu Gauss oleh penciptanya, matematikawan Jerman Carl F. Gauss (1777-1855). Operasi yang ditunjukkan setara dengan penentu matriks 2 × 2, misalnya penentu pertama adalah:

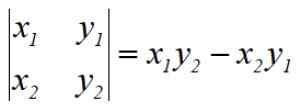
Untuk menemukan area Pentagon, kita harus menyelesaikan 5 penentu, tambahkan hasilnya secara aljabar, bagilah dengan 2 dan akhirnya mengekspresikan area selalu dengan tanda positif.

Latihan terpecahkan

Latihan 1

Temukan area Pentagon biasa yang apothemnya bernilai 4 cm dan yang mengukur sisi 5.9 cm.

Larutan

Karena itu adalah pentagon biasa, dan kami memiliki ukuran sisi dan apothem, kami menggunakan rumus yang dikurangi sebelumnya:

Dapat melayani Anda: Segitiga Scaleno

A = p x l_KE /2

Perimeter P sama dengan 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Latihan 2

Temukan area pentagon yang tidak teratur yang ditampilkan. Dimensi berikut diketahui:

Dc ≈ dari

Ae = ab = 5

BC = 12

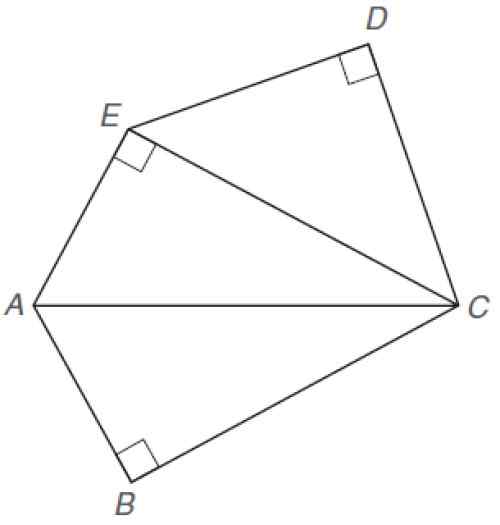Pentagon tidak teratur. Sumber: Alexander, D. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.

Larutan

Area Pentagon adalah jumlah dari area segitiga, yang merupakan persegi panjang. Pernyataan itu mengatakan bahwa DC ≈, oleh karena itu ketika menerapkan teorema Pythagoras ke segitiga EDC, ia memiliki:

Ec² = 2 ed². Kemudian EC = √2.Ed.

Segitiga AEC dan ABC memiliki hipotenuse yang sama, yang merupakan segmen AC, oleh karena itu:

Ea² + Ec² = Ab² + Bc²

Seperti EA dan AB mengukur hal yang sama, diperoleh itu:

Ec = bc = √2.Ed

Sejak BC = 12, maka ED = 12 / √2 = 8.485.

Dengan nilai -nilai ini kami akan menghitung luas setiap segitiga dan menambahkannya di akhir.

Area Segitiga EDC 

Ed x dc /2 = 8.485² / 2 = 36

Area segitiga AEC 

Ea x ec / 2 = ea x √2.Ed / 2 = 5 x √2. 8.485/2 = 30

Area Segitiga ABC 

AB X BC / 2

Maka daerah yang dicari adalah:

5 x 12/2 = 30

Itu sama dengan segitiga AEC, karena keduanya memiliki langkah yang sama.

Area Pentagon yang tidak teratur

Akhirnya area yang diminta adalah jumlah area dari tiga segitiga:

A = 36 + 30 + 30 unit = 96 unit.

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Referensi Terbuka Matematika. Area Poligon. Pulih dari: mathpenref.com.
3. Rumus alam semesta. Area pentagon yang tidak teratur. Pulih dari: universoformulas.com.
4. Rumus alam semesta. Area pentagon biasa. Pulih dari: universoformulas.com.
5. Wikipedia. Segi lima. Pulih dari: is.Wikipedia.com.