Formula aturan Simpson, demonstrasi, contoh, latihan

Itu Aturan Simpson Ini adalah metode untuk menghitung, kira -kira, integral yang ditentukan. Ini didasarkan pada membagi interval integrasi menjadi sepasang sub-intervalo yang sama-sama spasi.

Nilai ekstrem dari dua sub-interval berturut-turut mendefinisikan tiga titik, yang menyesuaikan parabola, yang persamaannya adalah polinomial tingkat kedua. 

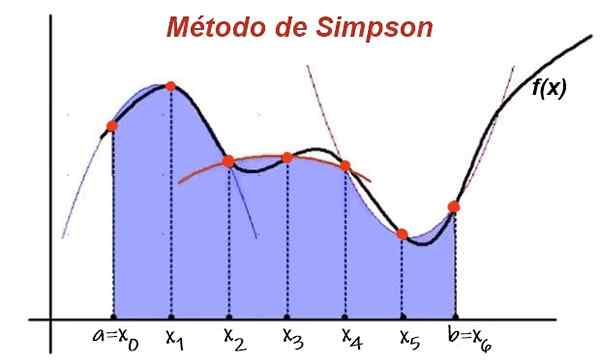
Gambar 1. Dalam metode Simpson, interval integrasi dibagi menjadi sepasang interval dengan lebar yang sama. Fungsi ini diperkirakan oleh perumpamaan di setiap 2 sub-intervalo dan pendekatan integral dengan jumlah area di bawah perumpamaan. Sumber: UPV.adalah.

Kemudian area di bawah kurva fungsi dalam dua interval berturut -turut diperkirakan oleh area polinomial interpolasi. Menambahkan kontribusi ke area di bawah perumpamaan semua sub-interval berturut-turut, ada nilai perkiraan integral.

Di sisi lain, karena integral dari suatu perumpamaan dapat dihitung secara aljabar secara persis, maka dimungkinkan untuk menemukan formula analitik untuk nilai perkiraan integral yang ditentukan. Dikenal sebagai Formula Simpson.

Kesalahan dari perkiraan hasil dengan demikian diperoleh berkurang sejauh jumlah subdivisi n lebih besar (menjadi n torsi) angka.

Di bawah ekspresi akan diberikan yang memungkinkan memperkirakan tingkat atas dari kesalahan pendekatan ke integral I, ketika partisi subinterval reguler dari interval total [a, b] telah dibuat [b].

[TOC]

Rumus

Interval integrasi [A, B] dibagi lagi menjadi N subinterval dengan n menjadi torsi. Lebar setiap subdivisi adalah:

H = (b - a)/n

Dengan cara ini, pada interval [a, b] partisi dibuat:

X0, x1, x2, ..., xn-1, xn

Menjadi x0 = a, x1 = x0 + h, x2 = x0 + 2h,…, xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Itu dapat melayani Anda: perbedaan antara lingkaran dan keliling (dengan contoh)

Rumus yang memungkinkan kira -kira menghitung fungsi integral dan kontinu yang ditentukan, dan lebih disukai lunak, dalam interval [a, b] adalah:

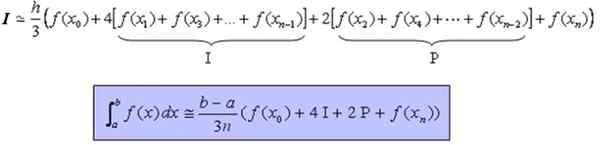
Demonstrasi

Untuk mendapatkan rumus Simpson, di setiap subinterval [xi, xi+2] fungsi F (x) mendekati dengan polinomial p (x) tingkat kedua yang melewati tiga poin: [xi, f (f (f (f (f (F (F (F (F (F (F (F (F (F (F (F (F (F xi)]; [Xi+1, f (xi+1)] dan [xi+2, f (xi+2)]]].

Maka polinomial integral P (x) dihitung dalam [xi, xi+2] yang mendekati integral fungsi f (x) dalam interval itu.

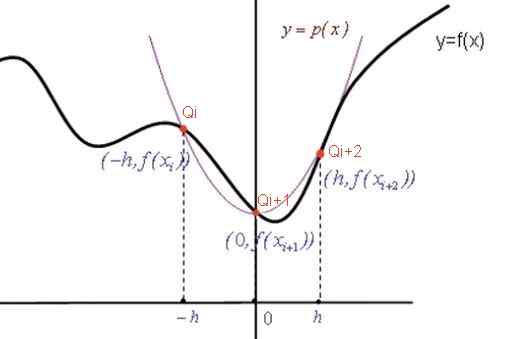Gambar 2. Grafik untuk menunjukkan formula Simpson. Sumber: f. Zapata.

Koefisien polinomial interpolasi

Persamaan Parabola P (x) memiliki bentuk umum: p (x) = a x² + B x + c. Saat perumpamaan melewati titik -titik yang ditunjukkan dalam warna merah (lihat gambar), maka koefisien a, b, c ditentukan dari sistem persamaan berikut:

AH)² - B h + c = f (xi)

C = f (xi+1)

AH)² + B h + c = f (xi + 2)

Dapat diamati bahwa koefisien C ditentukan. Untuk menentukan koefisien, kami menambahkan persamaan pertama dan ketiga mendapatkan:

2 a h² + 2 c = f (xi) + f (xi + 2).

Kemudian nilai C diganti dan jelas:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 jam²)

Untuk menentukan koefisien B, persamaan ketiga dari yang pertama dikurangi dan B membersihkan dirinya:

B = [f (xi+2) - f (xi)] = 2 h.

Singkatnya, polinomial tingkat kedua P (x) yang melewati titik -titik qi, qi+1 dan qi+2 memiliki koefisien:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 jam²)

B = [f (xi+2) - f (xi)] = 2 h

C = f (xi+1)

Perhitungan perkiraan integral dalam [xi, xi+2]

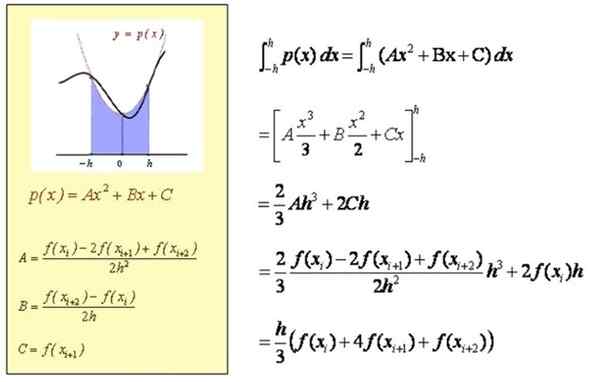
Perkiraan perhitungan integral dalam [a, b]

Seperti yang telah dikatakan, pada interval integrasi total [a, b] sebuah partisi x0, x1, x2,…, xn -1, xn dengan langkah h = xi+1 - xi = (b - (b -) / n, di mana n adalah pasangan.

Dapat melayani Anda: Kesalahan pengambilan sampel: Rumus dan persamaan, perhitungan, contoh

Kemudian integral yang didefinisikan dalam interval total [a, b] adalah jumlah integral dalam subinterval [xi, xi+2], yang didekati oleh integral polinomial interpolasi P (x):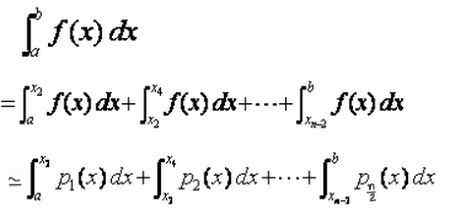

Pada bagian sebelumnya rumus untuk integral polinomial di subinterval ditemukan. Menerapkan hasil ini untuk setiap integral yang dimiliki: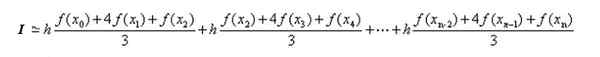

Yang dapat ditulis ulang dengan cara yang lebih kompak sebagai berikut: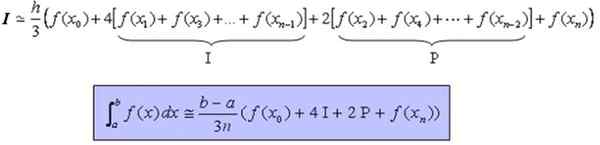

Kesalahan pendekatan

Jika fungsi yang ingin Anda integrasikan ke dalam interval [a, b] telah diturunkan ke urutan keempat, terus menerus dalam interval itu, maka dimungkinkan untuk menemukan rumus yang memungkinkan untuk menentukan tingkat kesalahan maksimum dalam pendekatan dengan cara dengan cara dari Formula Simpson SN Untuk nilai integral: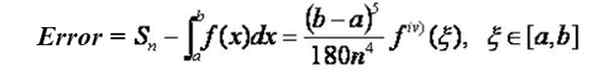

Perhatikan bahwa kesalahan berkurang dengan kekuatan keempat dari jumlah subdivisi interval. Misalnya, jika Anda beralih dari subdivisi N ke 2n, maka kesalahan berkurang dengan faktor 1/16.

Tingkat kesalahan atas yang diperoleh dengan pendekatan Simpson dapat diperoleh dari formula yang sama ini, mengganti turunan keempat dengan nilai absolut maksimum turunan keempat dalam interval [a, b].

Contoh terpecahkan

- Contoh 1

Pertimbangkan fungsi f (x) = 1 / (1 + x²). 

Temukan integral yang ditentukan dari fungsi F (x) dalam interval [-1, 1] menggunakan metode Simpson dengan dua subdivisi (n = 2).

Larutan 

Diambil n = 2. Batas integrasi adalah a = -1 dan b = -2, maka partisi seperti ini: 

X0 = -1; X1 = 0 dan x2 = +1.

Oleh karena itu, formula Simpson mengadopsi sebagai berikut:

Dengan n = 2 → xo = -1, x1 = 0; x2 = 1, oleh karena itu:

- Contoh 2

Pertimbangkan fungsi f (x) = 1 / (1 + x²). 

Temukan integral yang ditentukan dari fungsi f (x) dalam interval [-1, 1] dengan rumus Simpson dengan empat subdivisi (n = 4).

Itu dapat melayani Anda: estimasi berdasarkan interval

Larutan 

Diambil n = 4. Batas integrasi adalah a = -1 dan b = -2, maka partisi seperti ini: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 dan x4 = +1.

Formula Simpson ditetapkan sebagai berikut:

Integral ≃ [(b -a)/(3 n)] [f (x0) + 4 i + 2 p + f (xn)]]

Untuk kasus di mana ia diterapkan, itu adalah sebagai berikut:

Integral ≃ (1- (1))/(3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)

Integral ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1.5666

- Contoh 3

Tentukan integral yang didefinisikan dari contoh -contoh sebelumnya dengan tepat dan buat perbandingan hasil yang tepat dengan yang diperoleh dengan rumus Simpson dalam Contoh 1A dan 1B.

Larutan 

Integral tak terbatas dari fungsi f (x) = 1 / (1 + x²) adalah fungsinya Arctan (x).

Saat mengevaluasi batas integrasi:

Integral = arctan (1) - arctan (-1) = π/4 - (-π/4) = π/2 = 1.5708

Jika kita membandingkan hasil solusi yang tepat dengan yang diperoleh dengan metode Simpson dengan n = 2 dan n = 4 kita memiliki:

Untuk n = 2 perbedaan antara solusi yang tepat dan perkiraan adalah π/2 -5/3 = -0959, yaitu perbedaan persentase -0,06%.

Dan untuk pendekatan Simpson dengan n = 4, perbedaan antara persis dan solusi perkiraan adalah π/2 - 47/30 = 0,0041, yaitu perbedaan persentase 0,003%.

Latihan yang diusulkan

Metode Simpson cocok untuk diterapkan dalam bahasa pemrograman dan aplikasi komputer yang ditujukan untuk perhitungan matematika. Diusulkan kepada pembaca yang, berdasarkan rumus yang diberikan dalam artikel ini, menulis kodenya sendiri dalam program favoritnya.

Gambar berikut menunjukkan latihan di mana formula Simpson telah diimplementasikan Studio Smath, Perangkat lunak gratis tersedia untuk sistem operasi Windows Dan Android.

Gambar 3. Contoh integrasi numerik melalui aturan Simpson menggunakan perangkat lunak. Sumber: f. Zapata.

Referensi

1. Casteleiro, J. M. 2002. Perhitungan Komprehensif (Edisi Ilustrasi). Madrid: editorial ESIC.
2. Upv. Metode Simpson. Universitas Politeknik Valencia. Dipulihkan dari: YouTube.com
3. Purcell, e. 2007. Perhitungan Edisi Kesembilan. Prentice Hall.
4. Wikipedia. Aturan Simpson. Pulih dari: is.Wikipedia.com
5. Wikipedia. Interpolasi polinomial lagrange. Pulih dari: is.Wikipedia.com