Aturan Sturges

Kami menjelaskan apa aturan Sturges, aplikasinya dan memberikan beberapa contoh

Apa aturan Sturges?

Itu Aturan Sturges Ini adalah kriteria yang digunakan untuk menentukan jumlah kelas atau interval yang diperlukan untuk grafik satu set data statistik secara grafis. Aturan ini dinyatakan pada tahun 1926 oleh ahli matematika Jerman Herbert Sturges.

Sturges mengusulkan metode sederhana, berdasarkan jumlah sampel X yang memungkinkan untuk menemukan jumlah kelas dan rentang jangkauannya. Aturan Sturges banyak digunakan di atas semua di bidang statistik, khususnya untuk membangun histogram frekuensi.

Penjelasan

Aturan Sturges adalah metode empiris yang banyak digunakan dalam statistik deskriptif untuk menentukan jumlah kelas yang harus ada dalam histogram frekuensi, untuk mengklasifikasikan satu set data yang mewakili sampel atau populasi.

Pada dasarnya, aturan ini menentukan lebar wadah grafis, histogram frekuensi.

Untuk menetapkan aturannya, Herbert Sturges dianggap sebagai diagram frekuensi yang ideal, yang terdiri dari interval k, di mana interval i -ini berisi sejumlah sampel (i = 0, ... k - 1), diwakili sebagai:

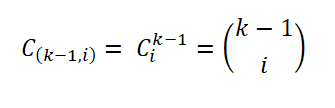
Jumlah sampel ini diberikan oleh jumlah cara di mana subset dari satu set dapat diekstraksi; yaitu, dengan koefisien binomial, dinyatakan sebagai berikut:

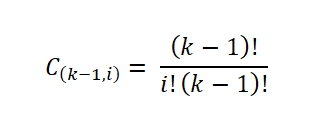Kemudian, sturges terkait bahwa histogram frekuensi akan mendekati distribusi normal ketika jumlah interval (k) meningkat sesuai dengan teorema pusat batas. Sedemikian rupa sehingga jumlah sampel dari masing -masing interval dapat dihitung:

Itu dapat melayani Anda: enegon: properti, cara membuat enegon, contoh

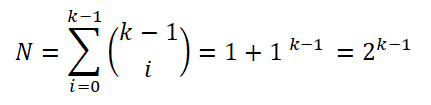
Untuk menyederhanakan ekspresi, ia menerapkan sifat -sifat logaritma di kedua bagian persamaan:

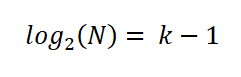
Dengan demikian, Sturges menetapkan bahwa jumlah interval K yang optimal diberikan oleh ekspresi:

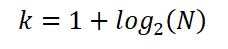
Itu juga dapat dinyatakan sebagai:

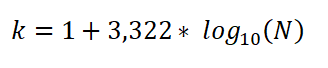
Dalam ungkapan ini:

• K adalah jumlah kelas.
• N adalah jumlah total pengamatan dalam sampel.
• Log adalah logaritma dasar umum 10.

Misalnya, untuk menguraikan histogram frekuensi yang mengekspresikan sampel acak perawakan 142 anak, jumlah interval atau kelas yang akan dimiliki distribusi adalah:

K = 1 + 3.322 _* catatan₁₀ (N)

K = 1+3.322_* Log (142)

K = 1+3.322_* 2.1523

K = 8.14 ≈ 8

Dengan demikian, distribusi akan dalam 8 interval.

Jumlah interval harus selalu diwakili oleh bilangan bulat. Dalam kasus di mana nilainya desimal, perkiraan harus dilakukan dengan bilangan bulat terdekat.

Aplikasi aturan Sturges

Aturan Sturges diterapkan terutama dalam statistik, karena memungkinkan distribusi frekuensi melalui perhitungan jumlah kelas (k), serta panjang masing -masing, juga dikenal sebagai amplitudo.

Amplitudo adalah perbedaan dalam batas atas dan bawah kelas, dibagi dengan jumlah kelas, dan dinyatakan:

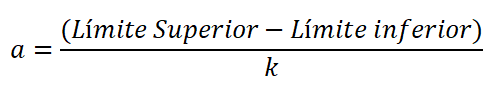
Ada banyak aturan empiris yang memungkinkan distribusi frekuensi. Namun, aturan Sturges umumnya digunakan karena membuat perkiraan jumlah kelas, yang biasanya berjalan dari 5 hingga 15.

Dengan cara ini, ia mempertimbangkan nilai yang dengan benar mewakili sampel atau populasi; Yaitu, pendekatan ini tidak mewakili kelompok ekstrem, juga tidak bekerja dengan sejumlah kelas yang berlebihan yang tidak memungkinkan untuk meringkas sampel.

Itu dapat melayani Anda: sudut yang berlawanan dengan simpul (dengan latihan terselesaikan)

Contoh

Histogram frekuensi perlu dilakukan sesuai dengan data yang diberikan, yang sesuai dengan usia yang diperoleh dalam survei pria yang berolahraga di gimnasium setempat.

Untuk menentukan interval, ukuran sampel atau jumlah pengamatan harus diketahui; Dalam hal ini, ada 30.

Kemudian aturan Sturges berlaku:

K = 1 + 3.322 _* catatan₁₀ (N)

K = 1+3.322_* Log (30)

K = 1+3.322_* 1.4771

K = 5,90 ≈ 6 interval.

Dari jumlah interval, Anda dapat menghitung amplitudo yang akan mereka miliki; Artinya, lebar setiap batang yang diwakili dalam histogram frekuensi:

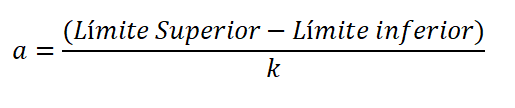
Batas bawah dianggap sebagai nilai data yang lebih rendah, dan bagian atas adalah nilai tertinggi. Perbedaan antara batas atas dan bawah disebut kisaran atau rute variabel (r).

Tabel memiliki batas atas adalah 46 dan 13 bawah; Dengan cara itu, amplitudo setiap kelas adalah:

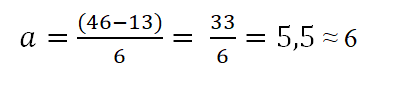
Interval akan terdiri dari batas atas dan bawah. Untuk menentukan interval ini, itu dimulai dengan menghitung dari batas bawah, menambah ini amplitudo yang ditentukan oleh aturan (6), sebagai berikut:

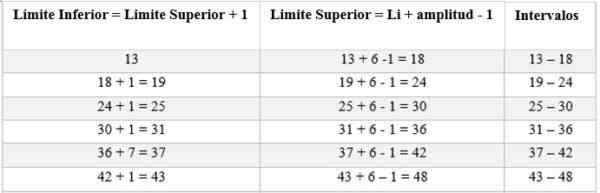
Maka frekuensi absolut dihitung untuk menentukan jumlah pria yang sesuai dengan setiap interval; Dalam hal ini adalah:

• Interval 1: 13 - 18 = 9
• Interval 2: 19 - 24 = 9
• Interval 3: 25 - 30 = 5
• Interval 4: 31 - 36 = 2
• Interval 5: 37 - 42 = 2
• Interval 6: 43 - 48 = 3

Dengan menambahkan frekuensi absolut dari setiap kelas, ini harus sama dengan jumlah total sampel; Dalam hal ini, 30.

Dapat melayani Anda: homotecia negatif

Selanjutnya, frekuensi relatif dari setiap interval dihitung, membagi frekuensi absolut ini dengan jumlah total pengamatan:

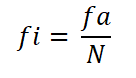
• Interval 1: fi = 9 ÷ 30 = 0,30
• Interval 2: Fi = 9 ÷ 30 = 0,30
• Interval 3: Fi = 5 ÷ 30 = 0,1666
• Interval 4: Fi = 2 ÷ 30 = 0,0666
• Interval 5: Fi = 2 ÷ 30 = 0,0666
• Interval 4: Fi = 3 ÷ 30 = 0.10

Kemudian Anda dapat membuat tabel yang mencerminkan data, dan juga diagram dari frekuensi relatif sehubungan dengan interval yang diperoleh, seperti yang dapat dilihat pada gambar berikut:

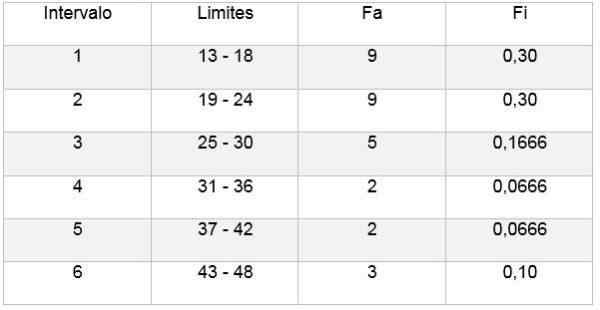
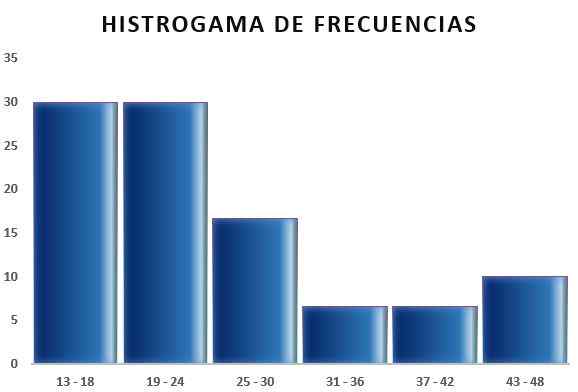
Dengan cara ini, aturan Sturges memungkinkan untuk menentukan jumlah kelas atau interval di mana sampel dapat dibagi, untuk merangkum sampel data melalui elaborasi tabel dan grafik.