Sistem oktal

Apa itu sistem oktal?

Dia Sistem oktal Ini adalah sistem penomoran dasar delapan (8); Yaitu, terdiri dari delapan digit, yaitu: 0, 1, 2, 3, 4, 5, 6 dan 7. Oleh karena itu, setiap digit angka oktal dapat memiliki nilai dari 0 hingga 7. Angka oktal dibentuk dari angka biner.

Ini karena basisnya adalah kekuatan yang tepat dari dua (2). Yaitu, angka -angka yang termasuk dalam sistem oktal terbentuk ketika dikelompokkan menjadi tiga digit berturut -turut, dipesan dari kanan ke kiri, sehingga mendapatkan nilai desimal mereka.

Sejarah sistem oktal

Sistem oktal berawal dari zaman kuno, ketika orang menggunakan tangan mereka untuk menghitung delapan dengan delapan hewan.

Misalnya, untuk menghitung jumlah sapi di kandang, tangan kanan mulai memiliki ibu jari dengan jari kelingking; Kemudian untuk menghitung hewan kedua, ibu jari datang bersama dengan jari telunjuk, dan seterusnya dengan jari -jari yang tersisa dari masing -masing tangan, sampai selesai 8.

Ada kemungkinan bahwa sistem penomoran oktal sebelum desimal untuk dapat menghitung ruang interdigital; yaitu, beri tahu semua jari kecuali untuk jempol.

Selanjutnya, sistem penomoran oktal didirikan, yang berasal dari sistem biner, karena membutuhkan banyak angka untuk mewakili hanya satu angka; Sejak saat itu, sistem oktal dan heksagonal dibuat, yang tidak memerlukan begitu banyak digit dan yang dapat dengan mudah dikonversi ke sistem biner.

Sistem penomoran oktal

Sistem oktal terdiri dari delapan digit mulai dari 0 hingga 7. Ini memiliki nilai yang sama seperti dalam kasus sistem desimal, tetapi nilai relatifnya berubah tergantung pada posisi yang ditempati. Nilai setiap posisi diberikan oleh kekuatan dasar 8.

Itu dapat melayani Anda: aturan t: karakteristik, sehingga itu, contoh

Posisi angka dalam angka oktal memiliki peso berikut:

8⁴, 8³, 8², 8¹, 8⁰, Titik oktal, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Digit oktal utama adalah 7; Dengan cara ini, ketika dihitung dalam sistem ini posisi satu digit dari 0 hingga 7 meningkat. Ketika mencapai 7 itu didaur ulang pada 0 untuk hitungan berikutnya; Ini meningkatkan posisi digit berikut. Misalnya, untuk menghitung urutan, dalam sistem oktal itu akan menjadi:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Ada teorema mendasar yang diterapkan pada sistem oktal, dan dinyatakan sebagai berikut:

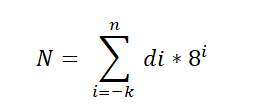
Dalam ungkapan ini di mewakili digit yang dikalikan dengan kekuatan dasar 8, yang menunjukkan nilai posisi setiap digit, dengan cara yang sama di mana ia dipesan dalam sistem desimal.

Misalnya, Anda memiliki angka 543.2. Untuk membawanya ke sistem oktal, ia terurai sebagai berikut:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0.125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_D

Dengan begitu Anda memiliki 543.2_Q = 354.25_D. Subskrip yang menunjukkan bahwa itu adalah nomor oktal yang juga dapat diwakili oleh nomor 8; dan Subscript D mengacu pada nomor desimal, yang juga dapat diwakili dengan nomor 10.

Konversi sistem oktal menjadi desimal

Untuk mengonversi nomor sistem oktal menjadi setara menjadi sistem desimal, setiap digit oktal harus dikalikan dengan nilai posisinya, mulai dari kanan.

Contoh 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Dapat melayani Anda: kesetaraan matematika

Contoh 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0.125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23.125₁₀

Konversi sistem desimal ke oktal

Integer desimal dapat dikonversi menjadi angka oktal menggunakan metode divisi yang diulang, di mana bilangan bulat desimal dibagi dengan 8 sampai hasil bagi sama dengan 0, dan pemborosan masing -masing divisi akan mewakili angka oktal.

Limbah diperintahkan dari yang terakhir ke yang pertama; yaitu, residu pertama akan menjadi angka paling tidak signifikan dari angka oktal. Dengan cara ini, digit yang paling signifikan akan menjadi residu terakhir.

Contoh

Octal dari nomor desimal 266₁₀

- Nomor Desimal 266 dibagi dengan 8 = 266/8 = 33 + 2 residu.

- Kemudian 33 dibagi dengan 8 = 33/8 = 4 + 1 residu.

- 4 dibagi dengan 8 = 4/8 = 0 + 4 residu.

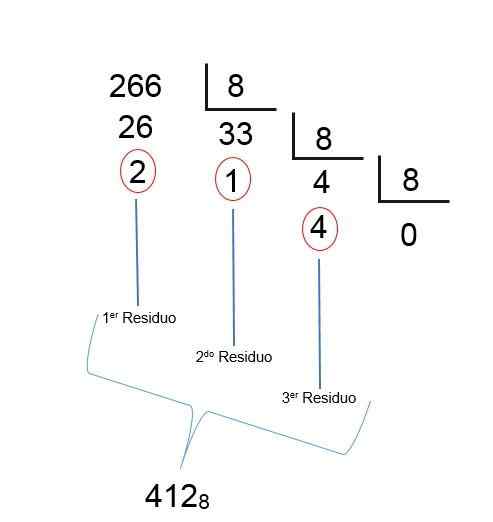
Seperti halnya divisi terakhir, hasil bagi kurang dari 1 diperoleh, itu berarti bahwa hasilnya telah ditemukan; Hanya sisa -sisa yang harus dipesan secara terbalik, sehingga jumlah oktal desimal 266 adalah 412, seperti yang dapat dilihat pada gambar berikut:

Konversi sistem oktal biner

Konversi sistem biner oktal dilakukan saat mengubah digit oktal menjadi digit biner yang setara, dibentuk oleh tiga digit. Ada tabel yang menunjukkan bagaimana delapan digit yang mungkin terjadi:

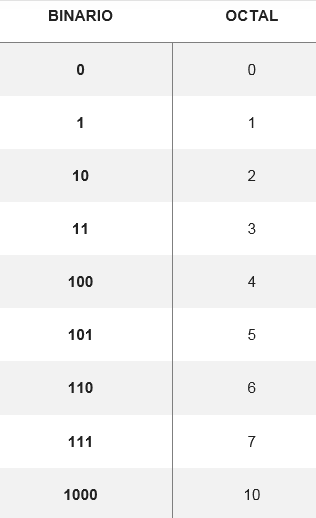
Dari konversi ini, Anda dapat mengubah sejumlah sistem oktal menjadi biner, seperti mengonversi nomor 572₈ Kesetaraan Anda dicari di tabel. Dengan demikian, Anda harus:

5₈ = 101

7₈= 111

2₈ = 10

Oleh karena itu, 572₈ setara dalam sistem biner dengan 10111110.

Sistem biner ke konversi oktal

Proses konversi angka integral ke bilangan bulat oktal adalah operasi terbalik ke proses sebelumnya.

Dapat melayani Anda: apa elemen sudut?

Artinya, bit bilangan biner dikelompokkan menjadi dua kelompok tiga bit, mulai dari kanan ke kiri. Kemudian, konversi biner ke oktal dibuat dengan tabel sebelumnya.

Dalam beberapa kasus, jumlah biner tidak akan memiliki kelompok 3 bit; Untuk menyelesaikannya, satu atau dua nol ditambahkan ke kiri grup pertama.

Misalnya, untuk mengubah nomor biner 11010110 menjadi oktal berikut ini dilakukan:

- Kelompok 3 bit dibentuk mulai dari kanan (bit terakhir):

11010110

- Karena grup pertama tidak lengkap, nol ditambahkan ke kiri:

011010110

- Konversi dibuat dari tabel:

011 = 3

010 = 2

110 = 6

Dengan cara ini, nomor biner 011010110 setara dengan 326₈.

Konversi sistem oktal menjadi heksadesimal dan sebaliknya

Untuk mengubah angka oktal ke heksadesimal atau heksadesimal ke sistem oktal, perlu bahwa angka itu pertama -tama akan menjadi biner, dan kemudian ke sistem yang diinginkan.

Untuk ini ada tabel di mana setiap digit heksadesimal diwakili dengan kesetaraannya dalam sistem biner, terdiri dari empat digit.

Dalam beberapa kasus, angka biner tidak akan memiliki kelompok 4 bit; Untuk menyelesaikannya, satu atau dua nol ditambahkan ke kiri grup pertama

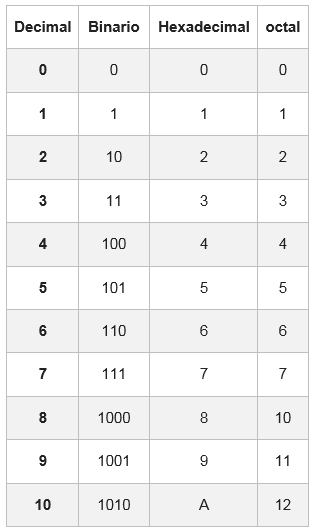
Contoh

Konversikan angka oktal 1646 menjadi angka heksadesimal:

- Angka oktal ke biner menjadi

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Jadi, 1646₈ = 1110100110.

- Untuk mengkonversi dari biner ke heksadesimal mereka pertama kali dipesan dalam kelompok 4 bit, mulai dari kanan ke kiri:

11 1010 0110

- Grup pertama diselesaikan dengan nol, sehingga dapat memiliki 4 bit:

0011 1010 0110

- Konversi sistem biner heksadesimal dibuat. Kesetaraan diganti dengan menggunakan tabel:

0011 = 3

1010 = a

0110 = 6

Dengan cara ini, angka oktal 1646 setara dengan 3a6 dalam sistem heksadesimal.