Suksesi majemuk

Suksesi terdiri dari kotak kuning dan biru. Sumber: f. Zapata

Apa itu suksesi gabungan?

A Suksesi majemuk Ini terdiri dari urutan elemen, dibuat dari dua (atau lebih) suksesi yang berbeda dan alternatif. Masing -masing suksesi ini memiliki aturan tertentu, yang digunakan untuk menemukan elemen masing -masing.

Elemen tidak harus numerik, bisa menjadi angka, simbol atau huruf, tetapi yang didasarkan pada angka disebut suksesi aritmatika. Sosok artikel kami dimulai menunjukkan suksesi majemuk dari kotak kuning dan biru.

Dalam suksesi ini, dimulai dari persegi besar yang terdiri dari 8 kotak kuning dan persegi biru. Untuk mendapatkan istilah berikut, kotak kuning ditambahkan ke kiri atau kanan dari barisan pertama dan ketiga kotak. Ruang yang menghasilkan baris tengah diisi dengan kotak biru.

Setiap gambar dalam urutan disebut ketentuan. Jika Anda ingin menemukan istilah kelima, Anda harus menambahkan kotak kuning di sebelah kanan peringkat pertama dan ketiga, dan kotak biru di baris kedua:

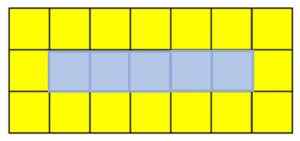Istilah kelima dari suksesi kotak kuning dan biru. Sumber: f. Zapata

Penjelasan

Dalam Succuctions Compound, Istilah diperoleh dengan mengganti ketentuan dua atau lebih suksesi sederhana yang independen. Untuk lebih memahami idenya, itu harus ditinjau detail dari suksesi sederhana.

Misalnya, suksesi sederhana berikut terdiri dari bilangan alami:

2, 4, 6, 8, 10, 12 ..

Poin -poin suspensi menunjukkan bahwa suksesi memiliki istilah yang tak terbatas.

Masing -masing istilah dilambangkan dengan surat kecil dan angka, sebagai subskrip. Angka ini menunjukkan posisi atau indeks dari setiap istilah. Dalam suksesi sebelumnya, Anda dapat menulis:

ke₁ = 2; ke₂ = 4; ke₃ = 6; ke₄ = 8 ..

Sangat nyaman untuk memiliki cara untuk menghitung istilah apa pun yang diinginkan dari suksesi, yaitu aturan khususnya. Dengan dia Istilah n-Ésimo, salah satu Istilah umum, dilambangkan sebagai_N.

Dapat melayani Anda: sifat kesetaraan

Melanjutkan dengan contoh suksesi angka genap, Anda dapat menetapkan cara untuk menghitung istilah n-Ésimo, dari istilah sebelumnya:

ke_N = a_N-1 + 2

Kemana_N-1 Itu adalah istilah yang mendahului_N.

Tentu saja akan lebih baik untuk mengetahui istilah umum tanpa bergantung pada persyaratan lainnya. Dalam suksesi ini mudah dicatat bahwa istilah apa pun dikalikan dengan 2 posisi yang ditempati, mengingat subskrip istilah. Dengan cara ini tertulis:

ke_N = 2n

Orang -orang Yunani kuno sudah tahu suksesi angka genap dan ganjil. Suksesi bilangan alami yang aneh, sementara itu, dapat ditulis sebagai:

1, 3, 5, 7, 9, 11 ..

Dan menggabungkan suksesi angka genap dengan yang aneh, suksesi senyawa berikut adalah:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Yang hasilnya merupakan himpunan bilangan alami.

Istilah suksesi majemuk

Mungkin menyenangkan untuk mencoba menemukan hubungan yang ada dalam urutan angka, yang harus diamati dengan cermat dan mencoba mengidentifikasi apakah itu adalah suksesi gabungan.

Bentuk umum dari suksesi yang terdiri dari dua suksesi adalah:

ke₁, B₁, ke₂, B₂, ke₃, B₃, ke₄, B₄,..

Kemana₁, ke₂, ke₃, ke₄,... adalah syarat dari suksesi pertama dan b₁, B₂, B₃, B₄,… Mereka yang kedua. Mereka selalu diselingi, seperti halnya dalam contoh ini:

7, 8, 14, 16, dua puluh satu, 24, 28, 32, 35..

Apa istilah yang mengikuti?

Untuk mengetahui, ketahui suksesi dalam dua set angka alternatif, sebagai berikut:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

Pada set pertama ini, kelipatan 7 muncul:

ke₁ = 7 × 1 = 7; ke₂ = 7 × 2 = 14; ke₃ = 7 × 3 = 21; ke₄ = 7 × 4 = 28; ke₅ = 7 × 5 = 35

Istilah umum dari suksesi ini adalah:

ke_N = 7n

Dan di yang kedua, ini adalah kelipatan 8:

B₁ = 8 × 1 = 8; B₂ = 8 × 2 = 16; B₃ = 8 × 3 = 24; B₄ = 8 × 4 = 32

Jadi istilah umumnya adalah:

Itu dapat melayani Anda: fungsi variabel nyata nyata dan representasi grafisnya

B_N = 8n

Kembali ke suksesi senyawa asli, 35 milik urutan pertama, yang istilahnya₁, ke₂, ke₃, ke₄ … 35 adalah istilah kelima, jadi istilah yang mengikuti harus b₅, yang mudah diperoleh dari aturan untuk menemukan istilah umum:

B₅ = 8 × 5 = 40

Dan itu tertulis:

7, 8, 14, 16, dua puluh satu, 24, 28, 32, 35, 40 ..

Contoh suksesi gabungan

Contoh 1

Anda dapat membuat suksesi gabungan dengan angka geometris, seperti kotak dan lingkaran, mengaturnya seperti yang ditunjukkan di bawah ini:

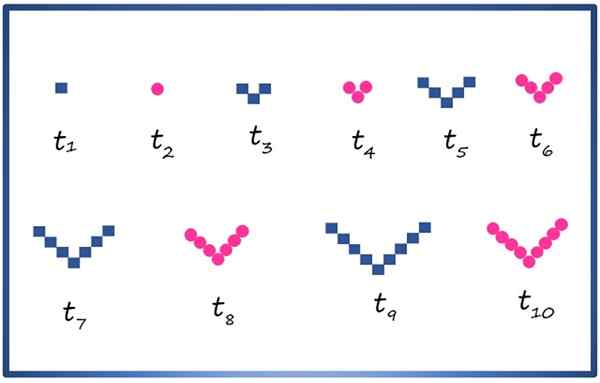10 istilah pertama dari suksesi gabungan dengan elemen dan lingkaran geometris persegi. Sumber: f. Zapata

Setiap istilah dilambangkan dengan t₁, T₂, T₃, T₄ …, Ketentuan Indeks Parque terdiri dari lingkaran dan indeks ganjil, kotak. Mengamati dengan hati -hati urutan yang dimungkinkan untuk mengetahui, misalnya, bahwa istilah t_sebelas, Itu tidak muncul di gambar, terdiri dari 11 kotak dengan ketentuan di v.

Contoh 2

Suksesi gabungan berikut terdiri dari simbol, dalam hal ini, huruf R dan S:

R SS RR SSS RRR SSS RRRR SSSS RRRR SSSSSS ..

Setiap istilah baru dibangun dengan menambahkan surat ke yang sebelumnya. Empat istilah pertama dari urutan yang ditampilkan adalah:

T₁= R ; T₂= H.H ; T₃= RR ; T₄= SSS ..

Dan istilah berikutnya yang akan muncul setelah istilah yang ditunjukkan adalah:

T_sebelas= Rrrrrr

Contoh 3

Contoh sebelumnya menunjukkan suksesi naik, di mana setiap nilai meningkat, dalam beberapa hal, sehubungan dengan sebelumnya. Tapi itu tidak selalu harus dengan cara ini, karena suksesi bisa turun, yaitu, mereka memiliki pola penurunan.

Dan suksesi naik dapat dikombinasikan dengan suksesi yang menurun.

Suksesi numerik berikut disusun:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Itu dapat dipisahkan menjadi dua suksesi:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Nilai apa yang harus ditempatkan di ruang kosong?

Mengamati dengan hati -hati suksesi pertama, setiap istilah diperoleh dengan menambahkan 3 ke istilah sebelumnya. Karena itu, ini adalah suksesi yang naik:

Dapat melayani Anda: perpindahan sudut

7 = 4 + 3

10 = 7 + 3

Karena itu, di ruang kosong pertama Anda harus menempatkan:

10 + 3 = 13

Setelah ini, istilah berikut, pada dasarnya:

16 = 13 + 3

Dan yang ada di bagian kosong kedua adalah:

16 + 3 = 19

Suksesi kedua menurun dan sangat mudah untuk menemukan istilah yang hilang, karena diamati bahwa setiap istilah diperoleh dengan mengurangi 1 dari istilah sebelumnya, oleh karena itu: oleh karena itu:

36, 35, 3. 4, 33, 32..

Akhirnya, Anda bisa menulis:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Latihan terpecahkan

Latihan 1

Dalam suksesi yang terdiri dari Contoh 3 di bagian sebelumnya:

a) Apakah 29 milik suksesi tersebut?

b) Tulis 10 istilah suksesi ini

Menjawab

Ya itu milik, karena suksesi kedua turun dan persyaratannya diperoleh dengan mengurangi 1 dari istilah sebelumnya. Dengan cara ini, akhirnya mencapai 29.

Jawaban b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Perhatikan bahwa beberapa istilah diulangi.

Latihan 2

Temukan istilah yang hilang dalam suksesi senyawa berikut:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Menjawab

Istilah aneh ditulis untuk mendapatkan suksesi pertama:

100, 115, 130, 145, 160, ..

Diamati bahwa, untuk menemukan setiap istilah, Anda harus menambahkan 15 ke istilah sebelumnya, oleh karena itu, istilah yang mengikuti pada 160 adalah 175.

Suksesi kedua terdiri dari:

500, 480, 460, 440, 420, ..

Setiap istilah berbeda dari yang sebelumnya dengan 20, suksesi yang turun, oleh karena itu, istilah yang diikuti pada 420 adalah 400.

Dengan informasi ini, dua istilah lagi ditambahkan ke suksesi senyawa asli, seperti ini:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Referensi

1. Larson, r. (2012). Prekalkulasi. Ke -8. Edisi. Pembelajaran Cengage.
2. Stewart, J. (2007). PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
3. Suksesi gabungan. Pulih dari: media.Educacioncampeche.Pelayar.MX.
4. Suksesi numerik. Diperoleh dari: Matemathweb.com.
5. Suksesi. Progresif aritmatika dan geometris. Diperoleh dari: MacMillanEducation.adalah.