Teori Karakteristik Set, Elemen, Contoh, Latihan

Itu Teori yang ditetapkan Ini adalah cabang dari logika-matematika yang bertanggung jawab untuk mempelajari hubungan antara entitas yang disebut set. Set ditandai dengan menjadi koleksi objek yang sama. Objek -objek ini adalah elemen dari himpunan dan dapat: angka, huruf, angka geometris, kata -kata yang mewakili objek, objek itu sendiri dan orang lain.

Itu adalah Georg Cantor, menjelang akhir abad ke -19, yang mengusulkan set set. Sementara ahli matematika terkemuka lainnya di abad kedua puluh membuat formalisasi mereka: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel antara lain.

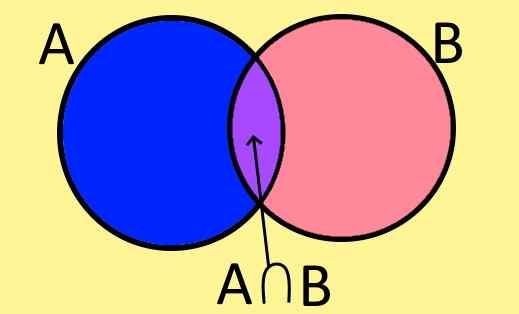
Gambar 1. Diagram Venn dari Set A, B dan persimpangan A⋂ B mereka. (Elaborasi sendiri).

Diagram Venn adalah cara grafis untuk mewakili satu set, dan terdiri dari figur datar tertutup di mana elemen set berada.

Sebagai contoh, Gambar 1 menunjukkan dua set A dan B, yang memiliki unsur -unsur yang sama, unsur -unsur umum untuk A dan B. Ini membentuk set baru yang disebut set persimpangan A dan B, yang ditulis secara simbolis sebagai berikut:

A ∩ B

[TOC]

Karakteristik

Set adalah konsep primitif seperti dalam geometri konsep titik, lurus atau datar. Tidak ada cara yang lebih baik untuk mengekspresikan konsep selain menunjukkan contoh: 

Set dan dibentuk oleh warna bendera Spanyol. Cara mengekspresikan set ini dipanggil dengan pemahaman. Set yang sama dan ditulis dengan ekstensi adalah:

E = merah, kuning

Dalam hal ini, merah dan kuning adalah elemen dari set dan. Perlu dicatat bahwa elemen -elemen tersebut tercantum di antara kunci dan tidak diulangi. Dalam kasus bendera Spanyol ada tiga garis warna (merah, kuning, merah) dua di antaranya diulang, tetapi elemen tidak diulang ketika set diekspresikan.

Asumsikan set V dibentuk oleh tiga huruf vokal pertama:

V = a, e, i

Kekuatan V, yang dilambangkan dengan P (V) adalah himpunan semua set yang dapat dibentuk dengan elemen V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Jenis set

Set terbatas

Itu adalah set di mana elemen -elemennya dapat dihitung. Contoh set terbatas adalah huruf alfabet Spanyol, vokal Spanyol, planet -planet tata surya antara lain. Jumlah elemen set terbatas disebut kardinalitasnya.

Set tak terbatas

Ensemble yang tak terbatas, setiap orang yang jumlah elemennya tidak dapat ditolak, karena terlepas dari seberapa besar jumlah elemennya selalu mungkin untuk menemukan lebih banyak elemen.

Contoh set tak terbatas adalah himpunan bilangan alami n, yang secara luas dinyatakan sebagai berikut:

Dapat melayani Anda: Coplanares Points: Persamaan, Contoh, dan Latihan Terpecahkan

N = 1, 2, 3, 4, 5, .. . jelas merupakan set yang tak terbatas, karena tidak peduli seberapa besar angka alami, jurusan berikut selalu dapat ditemukan dalam proses yang tak ada habisnya. Jelas kardinalitas set yang tak terbatas adalah ∞.

Set kosong

Itu adalah himpunan yang tidak mengandung elemen apa pun. Set V Empty dilambangkan dengan Ø atau dengan menggunakan satu kunci tanpa elemen di dalamnya:

V = = Ø.

Set kosong itu unik, oleh karena itu harus salah untuk mengatakan "set kosong", formulir yang benar adalah mengatakan "set kosong".

Di antara sifat -sifat set kosong, itu adalah subset dari set apa pun:

Ø ⊂ a

Selain itu, jika satu set adalah subset dari set kosong, maka set ini tentu akan menjadi batal:

A ⊂ Ø ⇔ A = Ø

Set kesatuan

Itu disebut set kesatuan set mana pun yang berisi satu elemen. Misalnya, himpunan satelit alami bumi adalah satuan unit, yang satu -satunya elemen adalah bulan. Set b dari bilangan bulat lebih kecil dari 2 dan lebih besar dari nol hanya memiliki elemen 1 oleh karena itu adalah set unit.

Set biner

Satu set adalah biner jika hanya memiliki dua elemen. Misalnya set x, sedemikian rupa sehingga x adalah jumlah nyata x^2 = 2 = 2. Set ini dengan ekstensi ditulis seperti ini:

X = -√2, +√2

Set universal

Set universal adalah set yang berisi set lain dari jenis atau alam yang sama. Misalnya, set universal bilangan alam adalah set bilangan real. Tetapi bilangan real juga universal dari bilangan bulat dan bilangan rasional.

Item inti

- Hubungan antar set

Di set Anda dapat membangun beberapa jenis hubungan antara mereka dan elemen mereka. Jika dua set A dan B memiliki elemen yang persis sama, di antaranya, hubungan yang sama dilambangkan sebagai berikut:

KE = B

Jika semua elemen dari himpunan untuk menjadi bagian dari set B, tetapi tidak semua elemen B milik A, maka di antara himpunan ini ada hubungan inklusi yang dilambangkan sebagai berikut:

A ⊂ B, tapi b ⊄ a

Ekspresi sebelumnya berbunyi: a adalah subset dari b, tetapi b bukan subset dari a.

Untuk menunjukkan bahwa beberapa atau beberapa elemen termasuk dalam satu set digunakan simbol kepemilikan ∈, misalnya untuk mengatakan bahwa elemen atau elemen x milik set A ditulis secara simbolis sebagai berikut:

x ∈ A

Ya sebuah elemen dan bukan milik set untuk hubungan ini ditulis seperti ini:

dan ∉ a

Hubungan kepemilikan diberikan antara elemen -elemen dari satu set dan set, dengan satu -satunya pengecualian dari set daya, set menjadi koleksi atau set semua set yang mungkin dapat dibentuk dengan elemen set tersebut.

Dapat melayani Anda: faktorisasi

Asumsikan v = a, e, i, kekuatan Anda adalah p (v) = a, e, i, a, e, a, i, e, i, a, e, i, dalam hal set v menjadi elemen dari himpunan p (v) dan dapat ditulis:

V ∈ P (V)

- Properti Inklusi

Properti pertama inklusi menetapkan bahwa setiap set terkandung dengan sendirinya, atau dengan kata lain, yang merupakan bagian dari dirinya sendiri:

A ⊂ a

Properti inklusi lainnya adalah transitivitas: jika A adalah subset dari B dan B pada gilirannya, itu adalah subset dari C, maka A adalah subset dari C. Symbolly Hubungan transitivitas ditulis seperti ini:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Di bawah ini adalah diagram Venn yang sesuai dengan transitivitas inklusi:

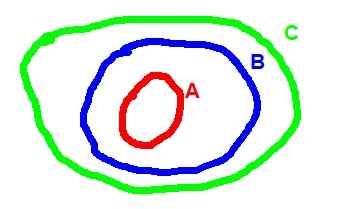Gambar 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Operasi antar set

Persimpangan

Persimpangan adalah operasi antara dua set yang menghasilkan set baru milik set universal yang sama dari dua yang pertama. Dalam hal itu, ini adalah operasi tertutup.

Secara simbolis, operasi persimpangan diformulasikan sebagai berikut:

A⋂b = x / x∈A ^ x∈B

Contohnya adalah sebagai berikut: Atur A dari huruf -huruf dalam kata "elemen" dan set b dari huruf kata "diulang", persimpangan antara A dan B ditulis seperti ini:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . Set universal A, dari B dan juga A⋂B adalah himpunan huruf alfabet Spanyol.

Persatuan

Persatuan dua set adalah set yang dibentuk oleh elemen yang umum untuk dua set dan elemen non -umum dari dua set tersebut. Operasi serikat antara set diekspresikan secara simbolis sebagai berikut:

A∪b = x/x∈A v x∈B

Perbedaan

Pengoperasian set setidaknya set dilambangkan dengan A-B. A-B adalah set baru yang dibentuk oleh semua elemen yang ada di A dan yang bukan milik B. Simbol ditulis seperti ini:

A - b = x/ x ∈ A ^ x ∉ b

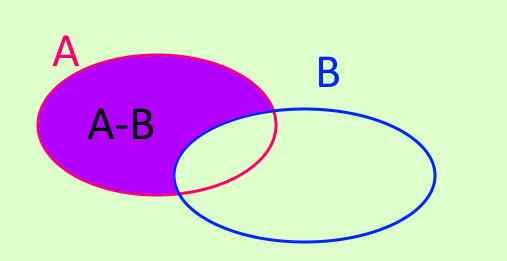Gambar 3. A - b = x/ x ∈ A ^ x ∉ b

Perbedaan simetris

Perbedaan simetris adalah operasi antara dua set di mana set yang dihasilkan terdiri dari elemen yang tidak umum untuk dua set. Perbedaan simetris secara simbolis direpresentasikan sebagai berikut:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Contoh

Contoh 1

Diagram Venn adalah cara grafis untuk mewakili set. Misalnya, set C dari huruf set kata diwakili sebagai berikut:

Contoh 2

Ini ditunjukkan di bawah ini melalui diagram Venn bahwa, himpunan vokal dalam kata "set", adalah subset dari himpunan huruf kata "set".

Dapat melayani Anda: Kuota Pengambilan Sampel: Metode, Keuntungan, Kekurangan, Contoh

Contoh 3

Mengatur N Dari huruf -huruf alfabet Spanyol itu adalah set yang terbatas, set ini dengan ekstensi ditulis seperti ini:

N = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z dan itu Kardinalitas adalah 27.

Contoh 4

Mengatur V Dari vokal dalam bahasa Spanyol itu adalah subset dari set:

V ⊂ N Oleh karena itu adalah set yang terbatas.

Set terbatas V Cara diperpanjang ditulis seperti ini: V = a, e, i, o, u dan kardinalitasnya 5.

Contoh 5

Mengingat set A = 2, 4, 6, 8 dan b = 1, 2, 4, 7, 9 Tentukan A-B dan B-A. 

A - B adalah elemen yang tidak ada dalam B:

A - b = 6, 8

B - A adalah elemen B yang tidak ada dalam:

B - A = 1, 7, 9

Latihan terpecahkan

Latihan 1

Tulis secara simbolik dan juga dengan ekstensi kelopak p dari bilangan alami bahkan lebih rendah dari 10.

Larutan: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Latihan 2

Asumsikan keseluruhan ke yang dibentuk oleh bilangan alami yang merupakan faktor 210, dan himpunan b yang dibentuk oleh bilangan alami sepupu lebih rendah dari 9. Tentukan kedua set dengan ekstensi dan tetapkan hubungan apa yang ada di antara kedua set tersebut.

Larutan: Untuk menentukan unsur -unsur set A, Anda harus mulai dengan menemukan faktor -faktor bilangan alami 210:

210 = 2 * 3 * 5 * 7

Kemudian set A ditulis:

A = 2, 3, 5, 7

Kami terus mempertimbangkan set B, yang merupakan sepupu yang lebih kecil dari 9. 1 bukan sepupu karena tidak memenuhi definisi sepupu: "Angka adalah sepupu jika dan hanya jika ia memiliki tepat dua pembagi 1 dan angka itu sendiri". 2 genap dan pada saat yang sama adalah sepupu karena memenuhi definisi sepupu, sepupu lain yang lebih kecil dari 9 adalah 3, 5 dan 7. Jadi set b adalah:

B = 2, 3, 5, 7

Oleh karena itu kedua set itu sama: a = B.

Latihan 3

Tentukan himpunan elemen -elemennya X berbeda dari x.

Larutan: C = x / x ≠ x

Seperti elemen apa pun, angka atau objek sama dengan dirinya sendiri, set C tidak bisa selain set kosong:

C = Ø

Latihan 4

Jadilah himpunan N bilangan alami dan z himpunan bilangan bulat. Tentukan n ⋂ z y n ∪ z.

Larutan: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z karena n ⊂ z.

Referensi

1. Garo, m. (2014). Matematika: Persamaan Kuadrat: Bagaimana Memecahkan Persamaan Kuadratik. Marilù Garo.
2. Haeussler, e. F., & Paul, R. S. (2003). Matematika untuk Administrasi dan Ekonomi. Pendidikan Pearson.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematika 1 Sep. Ambang.
4. Berharga, c. T. (2005). Kursus Matematika 3o. Progreso editorial.
5. Matematika 10 (2018). "Contoh set terbatas". Diperoleh dari: Mathematics10.bersih
6. Wikipedia. Teori yang ditetapkan. Pulih dari: is.Wikipedia.com