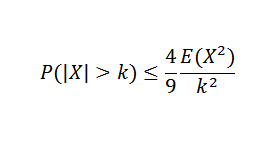Teorema Chebyshov yaitu, aplikasi dan contoh

Dia Teorema Chebyshov (atau ketidaksetaraan Chebyshov) adalah salah satu hasil klasik yang paling penting dari teori probabilitas. Ini memungkinkan memperkirakan probabilitas peristiwa yang dijelaskan dalam hal variabel acak x, dengan memberi kami tingkat yang tidak bergantung pada distribusi variabel acak tetapi pada varian x.

Teorema ini dipanggil untuk menghormati matematika Rusia.

Ketidaksetaraan ini, atau mereka yang karena karakteristiknya disebut ketidaksetaraan Chebyshov, terutama digunakan untuk memperkirakan probabilitas dengan cara menghitung level.

Apa teorema Chebyshov?

Dalam studi teori probabilitas, terjadi bahwa jika fungsi distribusi variabel acak x diketahui, nilai yang diharapkan dapat dihitung - atau harapan matematika dan (x) - dan variansnya var (x), selama ini jumlah ada. Namun, timbal balik belum tentu benar.

Yaitu, mengetahui e (x) dan var (x) tidak dapat selalu mendapatkan fungsi distribusi x, sehingga jumlah seperti p (| x |> k) untuk beberapa k> 0, sangat sulit diperoleh. Tapi terima kasih atas ketidaksetaraan Chebyshov, dimungkinkan untuk memperkirakan probabilitas variabel acak.

Teorema Chebyshov memberi tahu kita bahwa jika kita memiliki variabel acak x pada ruang sampel dengan fungsi probabilitas p, dan jika k> 0, maka:

Dapat melayani Anda: Acutangle Triangle

Aplikasi dan contoh

Di antara banyak aplikasi yang dimiliki Teorema Chebyshov, berikut ini dapat disebutkan:

1. Batas probabilitas

Ini adalah aplikasi yang paling umum dan digunakan untuk memberikan tingkat atas untuk p (| x-e (x) | ≥k) di mana k> 0, hanya dengan varians dan harapan variabel acak x, tanpa mengetahui fungsi probabilitas.

Contoh 1

Misalkan jumlah produk yang dibuat di perusahaan selama seminggu adalah variabel acak dengan rata -rata 50.

Jika diketahui bahwa varian satu minggu produksi sama dengan 25, maka apa yang dapat kita katakan tentang probabilitas bahwa minggu ini produksi berbeda dengan lebih dari 10 ke rata -rata?

Larutan

Menerapkan ketidaksetaraan Chebyshov kita harus:

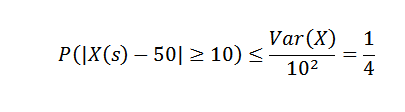
Dari sini kita dapat memperoleh bahwa probabilitas bahwa pada minggu produksi jumlah item melebihi lebih dari 10 hingga rata -rata paling 1/4.

2. Demonstrasi teori batas

Ketidaksetaraan Chebyshov memainkan peran penting dalam menunjukkan batas teori yang paling penting. Sebagai contoh, kami memiliki berikut ini:

Hukum yang lemah dalam jumlah besar

Undang -undang ini menetapkan bahwa diberikan suksesi x1, x2, ..., xn, ... dari variabel acak independen dengan distribusi rata -rata yang sama e (xi) = μ dan varians var (x) = σ², dan sampel rata -rata yang diketahui dari:

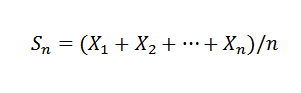
Jadi untuk k> 0 Anda harus:

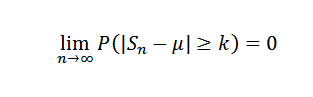
Atau setara:

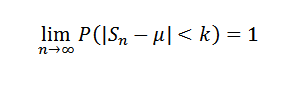
Demonstrasi

Pertama kita perhatikan yang berikut:

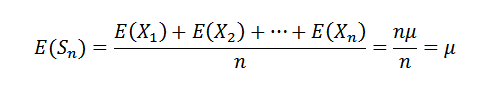
Seperti x1, x2, ..., xn independen, itu mengikuti itu:

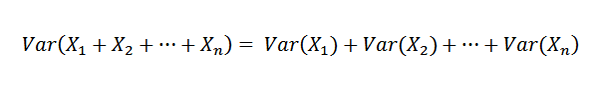
Oleh karena itu, dimungkinkan untuk menegaskan hal -hal berikut:

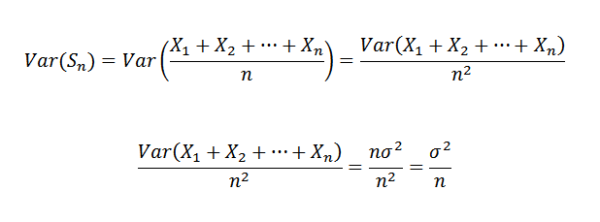
Kemudian, menggunakan teorema Chebyshov Anda harus:

Ini dapat melayani Anda: Fungsi Trigonometri: Dasar, di bidang Cartesian, Contoh, Latihan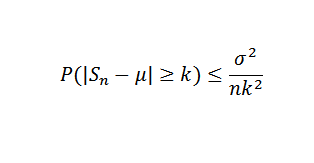

Akhirnya, teorema dihasilkan dari fakta bahwa batas yang tepat adalah nol ketika n cenderung tak terbatas.

Perlu dicatat bahwa tes ini dilakukan hanya untuk kasus di mana ada varian XI; yaitu, tidak menyimpang. Jadi kita mengamati bahwa teorema selalu benar jika e (xi) ada.

Teorema Batas Chebyshov

Jika x1, x2, ..., xn, ... itu adalah suksesi variabel acak independen sehingga ada beberapa C0:

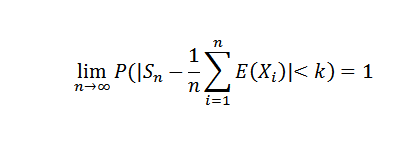
Demonstrasi

Karena suksesi varians terbatas secara seragam, kami memiliki var (Sn) ≤ C/N, untuk semua n alami. Tapi kita tahu itu:

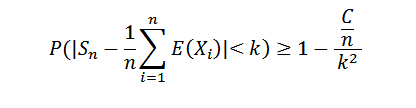
Membuat n menjadi tak terbatas, ini adalah sebagai berikut:

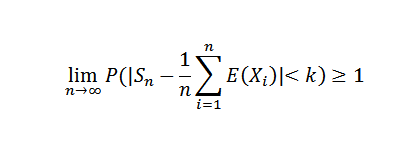
Karena probabilitas tidak dapat melebihi nilai 1, hasil yang diinginkan diperoleh. Sebagai konsekuensi dari teorema ini, kami dapat menyebutkan kasus Bernoulli tertentu.

Jika percobaan diulang secara independen dengan dua hasil yang mungkin (kegagalan dan keberhasilan), di mana P adalah probabilitas keberhasilan dalam setiap percobaan dan x adalah variabel acak yang mewakili jumlah keberhasilan yang diperoleh, maka untuk setiap k> 0 Anda harus:

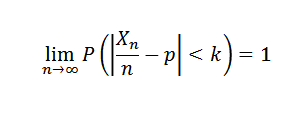
3. Ukuran sampel

Dalam hal varians, ketidaksetaraan Chebyshov memungkinkan kita untuk menemukan ukuran sampel yang cukup untuk memastikan bahwa probabilitas bahwa | sn-μ |> = k terjadi sekecil yang diinginkan, yang memungkinkan Anda memiliki pendekatan untuk tersebut rata-rata.

Tepatnya, baik itu x1, x2, ... xn Sampel variabel acak independen ukuran n dan anggaplah bahwa e (xi) = μ dan variansnya σ². Jadi, karena ketidaksetaraan Chebyshov, Anda harus:

Dapat melayani Anda: nomor atau angka euler e: berapa banyak ok, properti, aplikasi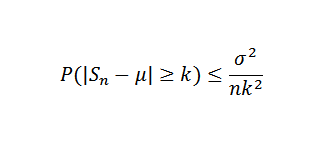

Sekarang menjadi Δ> 0 diperbaiki. Kita harus:

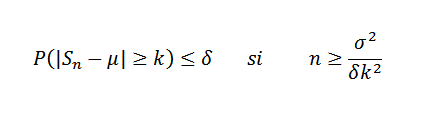
Contoh

Misalkan x1, x2, ... xn adalah sampel variabel acak independen dengan distribusi Bernoulli, sehingga mereka mengambil nilai 1 dengan probabilitas p = 0.5.

Apa yang seharusnya menjadi ukuran sampel untuk memastikan bahwa probabilitas bahwa perbedaan antara SN rata -rata aritmatika dan nilai yang diharapkan (yang melebihi lebih dari 0,1), kurang dari atau sama dengan 0.,01?

Larutan

Kita harus (x) = μ = p = 0,5 dan apa var (x) = σ²= P (1-p) = 0,25. Untuk ketidaksetaraan Chebyshov, untuk setiap k> 0 kita harus:

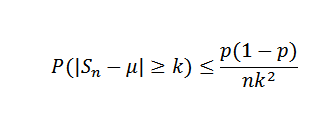
Sekarang, mengambil k = 0,1 dan Δ = 0,01, Anda harus:

Dengan cara ini disimpulkan bahwa ukuran sampel setidaknya 2500 diperlukan untuk memastikan bahwa probabilitas peristiwa | Sn - 0,5 |> = 0,1 kurang dari 0,01.

Jenis Ketimpangan Chebyshov

Ada berbagai ketidaksetaraan yang terkait dengan ketidaksetaraan Chebyshov. Salah satu yang paling terkenal adalah ketidaksetaraan Markov:

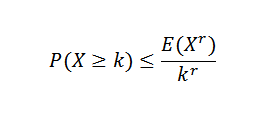
Dalam ungkapan ini x ini adalah variabel acak non -negatif dengan k, r> 0.

Ketimpangan Markov dapat mengambil bentuk yang berbeda. Misalnya, baik dan variabel acak non -negatif (jadi p (y> = 0) = 1) dan anggaplah bahwa E (y) = μ ada. Misalkan juga (e (y))^R= μ_R Ada beberapa integer r> 1. Jadi:

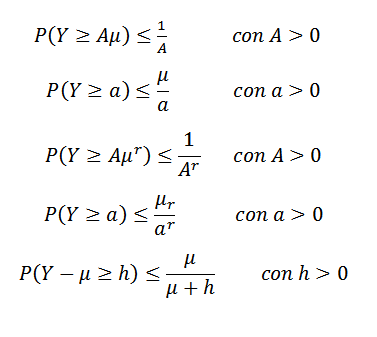
Ketidaksetaraan lainnya adalah Gauss, yang memberi tahu kita bahwa memberikan variabel acak X unimodal dengan fashion di nol, lalu untuk k> 0,