Jenis segitiga

Klasifikasi segitiga

Segitiga adalah sosok poligon atau geometris yang memiliki tiga sisi, tiga simpul dan tiga sudut. Sisi adalah masing -masing garis lurus yang membentuknya. Simpul adalah titik di mana sisi -sisi bergabung; Sudutnya adalah lengkungan atau bukaan yang terbentuk di dekat simpul, dengan bergabung dengan dua sisi.

Segitiga juga dapat didefinisikan sebagai area yang ditentukan oleh tiga baris. Jumlah dari tiga sudutnya selalu sama dengan 180º. Panjang salah satu sisinya selalu kurang dari hasil dari jumlah panjang dua sisi lainnya, tetapi lebih besar dari pengurangannya.

Segitiga adalah tokoh geometris yang paling sederhana, dan berfungsi untuk menyelidiki sifat matematika dari tokoh -tokoh lain yang lebih kompleks, seperti pentagon atau heksagon.

Mereka juga digunakan dalam ilmu lain, seperti topografi, navigasi atau astronomi. Di yang terakhir mereka terbiasa mengetahui jarak yang memisahkan kita dari tubuh biru muda yang jauh dari dua titik pengamatan yang terletak di Bumi. Metode ini dikenal sebagai paralase.

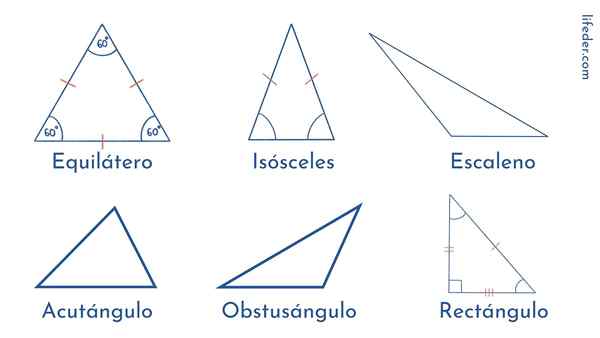
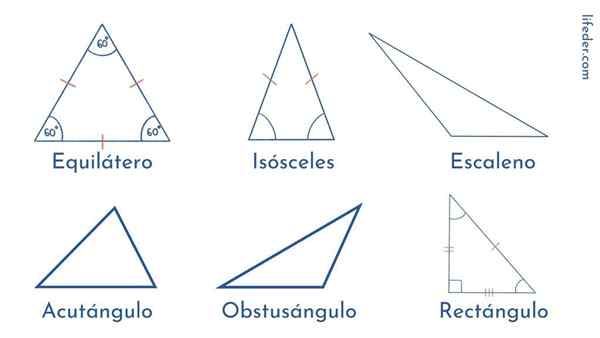
Segitiga diklasifikasikan sesuai dengan panjang sisi mereka atau sesuai dengan amplitudo sudut mereka.

Jenis Segitiga Menurut Sisi Mereka

Segitiga sama sisi

Sisi jenis segitiga ini memiliki panjang yang persis sama. Dan hal yang sama berlaku untuk sudut mereka: ketiganya 60º. Itulah sebabnya kami mengatakan bahwa segitiga sama sisi adalah poligon biasa.

Segitiga Scalene

Berbeda dengan sisi, dalam segitiga scalene semuanya tidak setara: ketiga sisi memiliki panjang yang berbeda dan sudutnya berbeda dalam amplitudo.

Dapat melayani Anda: Operasi gabungan

Segitiga sama kaki

Dalam jenis segitiga ini kami menemukan bahwa dua sisi memiliki ukuran yang sama, sedangkan sisi yang tersisa berbeda. Hal yang sama diamati dalam amplitudo sudut: dua sama dan satu berbeda.

Jenis segitiga sesuai dengan sudutnya

Segitiga siku-siku

Ini ditandai dengan memiliki sudut yang tepat, yaitu 90º. Dua sudut lainnya akut atau kurang dari 90º.

Dalam jenis segitiga ini, sisi terpanjang disebut hypotenusa, sedangkan dua sisi lainnya adalah kategori.

Segitiga miring

Segitiga yang tidak memiliki sudut kanan milik jenis ini. Mereka dibagi menjadi dua jenis:

Acutangle Triangle: Tiga sudutnya akut.

Segitiga tumpul: Mereka memiliki dua sudut akut dan satu yang jelas atau lebih besar dari 90º.

Segitiga campuran

Segitiga yang sama dapat diklasifikasikan sesuai dengan dua kriteria, yaitu, sesuai dengan panjang sisi mereka dan amplitudo sudut mereka.

Misalnya, segitiga persegi panjang juga bisa Escalano atau Isosceles, tetapi tidak bisa sama -sama, karena yang terakhir tidak menghadirkan sudut kanan apa pun.

Namun, segitiga sama sisi bisa akut, karena secara efektif memiliki tiga sudut akut atau kurang dari 90º.

Segitiga tumpul scalene

Segitiga scalene dapat didatangkan, karena baik amplitudo sudutnya dan panjang sisinya berbeda.

Cara menghitung perimeter segitiga?

Produk dari jumlah panjang tiga sisi segitiga disebut perimeter.

Mari kita lihat beberapa contoh.

1- Kami diminta untuk menemukan perimeter segitiga scalene yang sisinya 6, 8 dan 4 sentimeter. Yang harus kita lakukan adalah menambahkan:

Dapat melayani Anda: konstanta absolut

6 + 8 + 4 = 18

Oleh karena itu, perimeter segitiga scalene ini adalah 10 sentimeter.

2- Lalu mereka meminta kami untuk menghitung perimeter dari segitiga isosceles yang sisi-sisinya mengukur 4 sentimeter dua dan 6 sentimeter sisi yang tersisa. Karena dua sisinya memiliki panjang yang sama, kita harus menempatkan sosok yang sama dua kali, seperti ini:

4 + 4 + 6 = 14

Perimeter segitiga ini adalah 14 sentimeter.

3- Contoh terakhir. Kami memiliki tugas untuk menentukan perimeter segitiga sama sisi 9 sentimeter ke samping. Seperti yang kita ketahui karakteristik dari berbagai jenis segitiga, kita tahu bahwa halal dibedakan karena ketiga sisinya sama. Karena itu:

9 + 9 + 9 = 27

Perimeter dari sisi ini adalah 27 sentimeter.

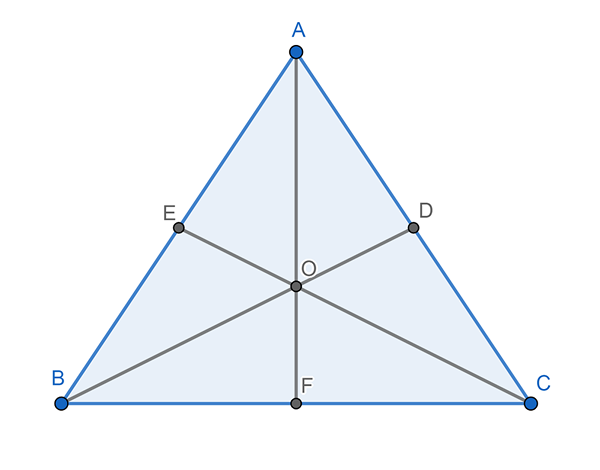
Mediatrices, bisector dan medium

Ini adalah tiga jenis garis lurus yang dapat ditarik dalam segitiga.

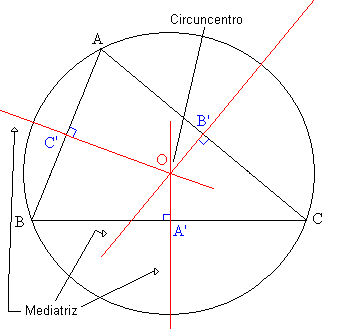
Mediatrices

Ada tiga, satu di setiap sisi segitiga. Mediatrix adalah garis lurus yang melewati titik tengah sisi segitiga yang sesuai. Tiga mediatrices dari segitiga berpotongan pada titik yang dikenal sebagai circumcentro, yang pada jarak yang sama dari masing -masing simpul segitiga.

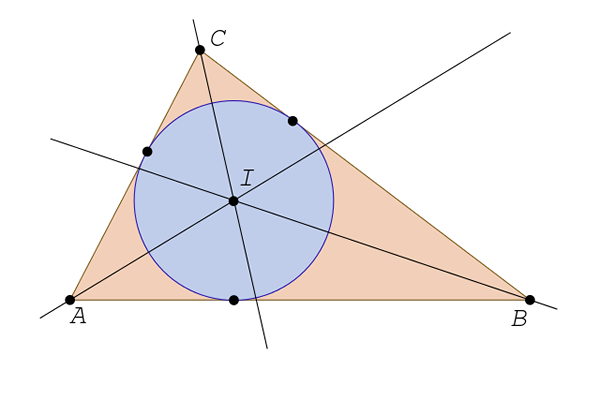
Bisektor

Ada tiga, satu untuk setiap sudut. Bisector adalah garis lurus yang dimulai dari simpul dan membagi sudut menjadi dua bagian yang sama. Para bisektor dari segitiga berpotongan pada titik yang dikenal sebagai insenter.

Sedang

Ada juga tiga, satu untuk setiap simpul. Median adalah garis yang dimulai dari titik dan mencapai titik tengah di sisi yang berlawanan. Median segitiga bersinggungan pada suatu titik yang disebut Baricentro.

Dapat melayani Anda: Kesalahan pengambilan sampel: Rumus dan persamaan, perhitungan, contoh

Jarak antara salah satu dari tiga simpul dan BaryCenter setara dengan dua pertiga (2/3) dari total panjang median yang sesuai. Misalnya, jika median CE berukuran 5 sentimeter, maka jarak antara C dan pusat baricenter (O) sama dengan 5 x 2/3, atau apa yang sama, 5 x 0,66, yang menghasilkan 3, 3 sentimeter.

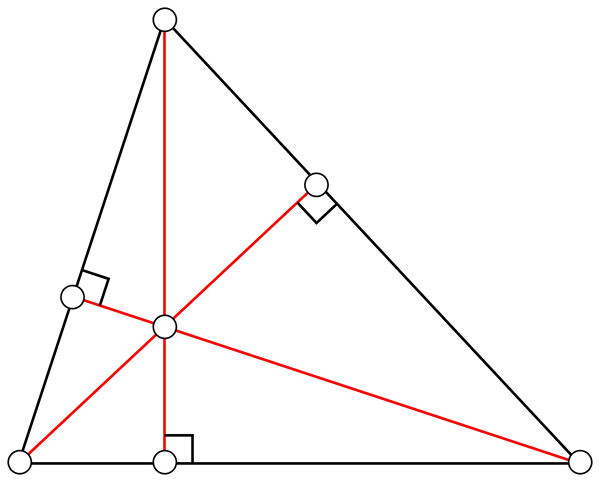
Ketinggian

Itu adalah garis lurus yang bergabung dengan simpul dengan sisi yang berlawanan. Tiga ketinggian segitiga berpotongan pada titik yang disebut ortotroenter. Tergantung pada jenis segitiga, orthocenter dapat berada di dalam atau di luar area segitiga.

Cara menghitung area segitiga?

Area segitiga apa pun dapat diketahui saat menerapkan formula berikut:

A = b x h / 2

Dalam persamaan ini, A mengacu pada area tersebut; B mengacu pada pangkalan dan h adalah ketinggian.

Mari kita lihat sebuah contoh. Kami diminta untuk menghitung luas segitiga yang pangkalannya berukuran 12 sentimeter dan tingginya 7 sentimeter. Jadi, kami memiliki:

B = 12

H = 7

Kami menerapkan formula:

A = 12 x 7/2

A = 84/2

A = 44

Oleh karena itu, segitiga ini memiliki luas 44 sentimeter persegi.