Lintasan dan perpindahan

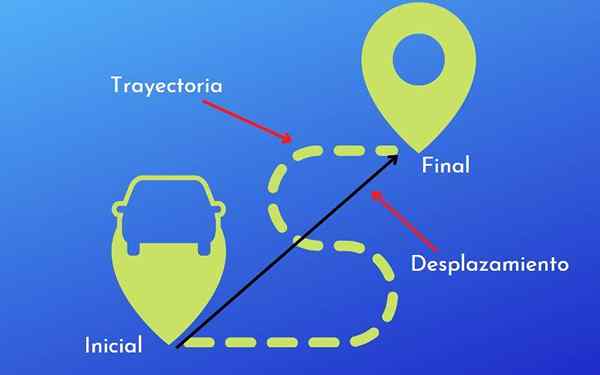
Perbedaan antara lintasan dan perpindahan. Dengan lisensi

Itu Perbedaan antara lintasan dan perpindahan adalah bahwa yang terakhir adalah jarak dan arah yang ditempuh oleh suatu objek, sedangkan lintasan adalah rute atau bentuk yang diadopsi oleh pergerakan objek itu.

Namun, untuk melihat lebih jelas perbedaan antara perpindahan dan lintasan, lebih baik menjelaskan melalui contoh -contoh yang memungkinkan pemahaman yang lebih besar dari kedua istilah.

Pemindahan

Itu dipahami sebagai jarak dan arah yang ditempuh oleh suatu objek, dengan mempertimbangkan posisi awal dan posisi terakhirnya, selalu dalam garis lurus. Untuk perhitungannya, karena merupakan besarnya vektor, pengukuran panjang yang dikenal sebagai sentimeter, meter atau kilometer digunakan.

Rumus untuk menghitung perpindahan didefinisikan sebagai berikut:

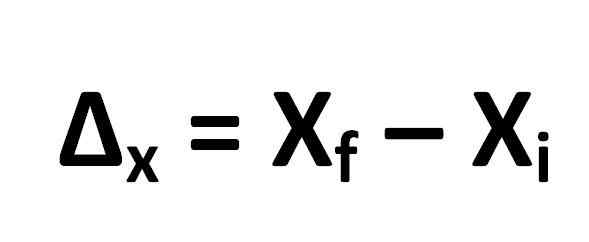
Dari mana itu mengikuti itu:

- Δ_X = perpindahan

- X_F = posisi akhir objek

- X_yo = posisi objek awal

Contoh perpindahan

1. Jika sekelompok anak berada di awal rute, yang posisi awalnya adalah 50 m, bergerak dalam garis lurus, menentukan perpindahan di masing -masing titik x_F. 

- X_F = 120 m

- X_F = 90 m

- X_F = 60 m

- X_F = 40 m

2. Data masalah diekstraksi dengan mengganti nilai x₂ dan x₁ Dalam formula perpindahan:

- Δ_X = ?

- X_yo = 50 m

- Δ_X = X_F - X_yo

- Δ_X = 120 m - 50 m = 70 m

3. Dalam pendekatan pertama ini kami mengatakan bahwa Δ_X Itu sama dengan 120 m, yang sesuai dengan nilai pertama yang kita temukan dari x_F, kurang 50 m yang merupakan nilai x_yo, Itu menghasilkan 70 m, yaitu, saat mencapai 120 m bepergian, perpindahan adalah 70 m ke kanan.

Dapat melayani Anda: Cabang Laboratorium

4. Kami melanjutkan untuk menyelesaikan dengan cara yang sama untuk nilai B, C dan D

- Δ_X = 90 m - 50 m = 40 m

- Δ_X = 60 m - 50 m = 10 m

- Δ_X = 40 m - 50 m = - 10 m

Dalam hal ini perpindahan memberi kami negatif, itu berarti bahwa posisi akhir berada dalam arah yang berlawanan dari posisi awal.

Lintasan

Ini adalah rute atau garis yang ditentukan oleh suatu objek selama pergerakan dan penilaiannya dalam sistem internasional, ia umumnya mengadopsi bentuk geometris seperti garis, perumpamaan, lingkaran atau elips.

Itu diidentifikasi melalui garis imajiner dan dengan menjadi kuantitas skalar diukur dalam meter.

Perlu dicatat bahwa untuk menghitung lintasan yang harus kita ketahui jika tubuh sedang istirahat atau bergerak, yaitu, itu diserahkan ke sistem referensi yang kita pilih.

Persamaan untuk menghitung lintasan suatu objek dalam sistem internasional diberikan oleh:

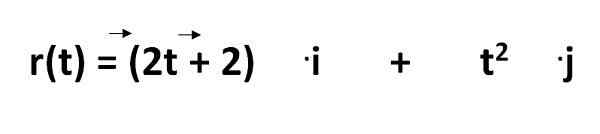
Yang harus kita lakukan:

- R (t) = Ini adalah persamaan lintasan

- 2t - 2 dan t² = mewakili koordinat sebagai fungsi waktu

-  ^.saya dan ^.J = adalah vektor unit

Untuk memahami perhitungan lintasan yang dilalui oleh suatu objek, kami akan mengembangkan contoh berikut:

Hitung persamaan lintasan vektor posisi berikut:

- R (t) = (2t + 7) ^.i + t^{2 .}J

- R (t) = (t - 2) ^.R&D 2T ^.J

Langkah Pertama: Sebagai persamaan lintasan adalah fungsi x, untuk ini untuk menentukan nilai -nilai x dan y masing -masing di masing -masing vektor yang diangkat:

1. Selesaikan vektor posisi pertama:

- R (t) = (2t + 7) ^.i + t^{2 .}J

2. Ty = f (x), di mana x diberikan oleh konten vektor unit ^.Saya dan diberikan oleh konten vektor unit ^.J:

Dapat melayani Anda: ad hoc: asal istilah, makna dan contoh penggunaan

- X = 2t + 7

- Y = t²

3. y = f (x), yaitu, waktu bukan bagian dari ekspresi, oleh karena itu, kita harus menghapusnya, kita memiliki:

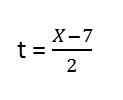
4. Kami mengganti izin dan. Tetap:

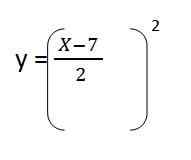
5. Kami memecahkan konten tanda kurung dan kami memiliki persamaan lintasan yang dihasilkan untuk vektor unit pertama:

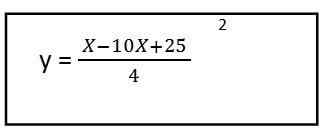
Seperti yang bisa kita lihat, itu menghasilkan persamaan tingkat kedua, ini berarti bahwa lintasan adalah untuk bentuk parabola.

Langkah Kedua: Kami melanjutkan dengan cara yang sama untuk perhitungan lintasan vektor unit kedua:

1. R (t) = (t - 2) ^.R&D 2T ^.J

- X = t - 2

- Y = 2t

2. Mengikuti langkah -langkah yang kita lihat sebelumnya y = f (x), kita harus menghapus waktu karena itu bukan bagian dari ekspresi, kita memiliki:

- t = x + 2

3. Kami mengganti izin masuk dan, tetap:

- y = 2 (x + 2)

4. Memecahkan tanda kurung, kami memiliki persamaan lintasan yang dihasilkan untuk vektor unit kedua:

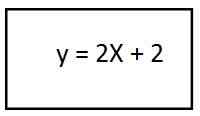
Dalam prosedur ini kami menghasilkan garis, yang memberi tahu kami bahwa lintasan memiliki bentuk bujursangkar.

Memahami konsep perpindahan dan lintasan kita dapat menyimpulkan sisa perbedaan yang ada antara kedua istilah.

Lebih banyak perbedaan antara perpindahan dan lintasan

Pemindahan

- Itu adalah jarak dan arah yang ditempuh oleh suatu objek dengan mempertimbangkan posisi awal dan posisi terakhirnya.

- Selalu terjadi dalam garis lurus.

- Diakui dengan panah.

- Gunakan ukuran panjang (sentimeter, meter, kilometer).

- Itu adalah jumlah vektor.

- Mempertimbangkan arah yang ditempuh (kanan atau kiri)

- Tidak mempertimbangkan waktu yang dihabiskan selama tur.

Dapat melayani Anda: kondensasi: konsep, proses, contoh

- Itu tidak tergantung pada sistem referensi.

- Ketika titik awal adalah titik awal yang sama, perpindahannya nol.

- Modul harus bertepatan dengan ruang untuk di -tur selama lintasan adalah garis lurus dan tidak ada perubahan dalam arti untuk diikuti.

- Modul cenderung meningkat atau berkurang saat gerakan terjadi, dengan mempertimbangkan lintasan.

Lintasan

Itu adalah rute atau garis yang ditentukan oleh suatu objek selama gerakannya. Mengadopsi bentuk geometris (lurus, parabola, melingkar atau elips).

- Itu diwakili melalui garis imajiner.

- Diukur dalam meter.

- Itu adalah kuantitas skalar.

- Tidak memperhitungkan cara bepergian.

- Pertimbangkan waktu yang dihabiskan selama tur.

- Itu tergantung pada sistem referensi.

- Ketika titik awal atau posisi awal sama dengan posisi akhir, lintasan diberikan oleh jarak yang ditempuh.

- Nilai lintasan bertepatan dengan modul perpindahan vektor, jika lintasan yang dihasilkan adalah garis lurus, tetapi tidak ada perubahan dalam arti untuk diikuti.

- Itu selalu meningkat ketika tubuh bergerak, terlepas dari lintasannya.

Referensi

1. Fernández, m., Fidalgo, J. (2016). Fisika dan Kimia 1st Baccalaureate. Edisi paraninfo, s.KE. Spanyol.
2. Institut Pendidikan Radio Guatemala (2011) Fisika Fundamental. Grup Semester Zaculeu Pertama. Guatemala.