Perhitungan vektor penyeimbang, contoh, latihan

Dia Vektor menyeimbangkan Itu adalah yang kontras dengan vektor yang dihasilkan dan oleh karena itu ia dapat menyeimbangkan suatu sistem, karena memiliki besarnya yang sama dan arah yang sama, tetapi bertentangan dengan ini.

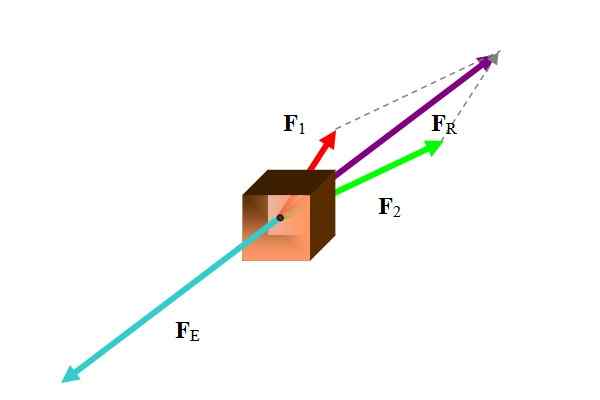
Pada banyak kesempatan, vektor penyeimbang mengacu pada vektor gaya. Untuk menghitung gaya penyeimbang, gaya yang dihasilkan adalah yang pertama, seperti yang ditunjukkan pada gambar berikut:

Gambar 1. Pada tubuh dua kekuatan tindakan yang hasilnya diseimbangkan dengan paksa dalam warna pirus. Sumber: Made sendiri.

Ada berbagai metode untuk melakukan tugas ini, sesuai dengan data yang ada. Karena kekuatannya adalah vektor, hasilnya adalah jumlah vektor dari kekuatan yang berpartisipasi:

F_R = F₁ + F₂ + F₃ +  .. .

Di antara metode yang akan digunakan adalah metode grafis seperti metode poligonal, jajaran genjang dan analitik seperti dekomposisi kekuatan dalam komponen Cartesian mereka. Dalam contoh gambar digunakan, metode jajaran genjang.

Setelah gaya yang dihasilkan ditemukan, gaya penyeimbang justru vektor yang berlawanan.

Ya F_DAN Itu adalah kekuatan penyeimbang, maka itu terpenuhi itu F_DAN Diterapkan pada titik tertentu, ia menjamin keseimbangan terjemahan sistem. Jika itu adalah partikel tunggal, ia tidak akan bergerak (atau mungkin ia melakukannya dengan kecepatan konstan), tetapi jika itu adalah objek yang diperluas, ia masih akan memiliki kemungkinan berbalik:

F_R + F_DAN = 0

[TOC]

Contoh

Kekuatan penyeimbang hadir di semua sisi. Kita sendiri diseimbangkan oleh kekuatan yang diberikan kursi untuk mengimbangi berat badan. Objek yang ditemukan saat istirahat: buku, furnitur, lampu langit -langit dan sejumlah besar mekanisme, terus -menerus diimbangi oleh kekuatan.

Dapat melayani Anda: guncangan inelastik: dalam dimensi dan contoh

Misalnya, buku istirahat di atas meja diseimbangkan oleh gaya normal yang diberikannya pada buku, mencegahnya jatuh. Hal yang sama berlaku untuk rantai atau kabel yang menahan lampu yang menggantung dari langit -langit di sebuah ruangan. Kabel yang menahan beban didistribusikan beratnya melalui ketegangan di dalamnya.

Dalam cairan beberapa objek dapat mengapung dan tetap diam, karena beratnya seimbang oleh gaya naik yang diberikan oleh cairan, yang disebut dorongan.

Berbagai mekanisme harus seimbang mengetahui vektor gaya penyeimbang seperti batang, balok dan kolom.

Saat menggunakan keseimbangan, entah bagaimana menyeimbangkan berat objek dengan gaya yang setara, baik menambahkan bobot atau dengan pegas.

Tabel kekuatan

Tabel gaya digunakan di laboratorium untuk menentukan gaya seimbang. Ini terdiri dari platform melingkar, di mana Anda memiliki pandangan atas pada gambar, dan yang memiliki transporter untuk mengukur sudut.

Di tepi meja ada katrol di mana string yang menahan bobot dan yang menyatu dalam lingkaran yang ada di tengah.

Misalnya dua bobot digantung. Ketegangan yang dihasilkan pada senar oleh bobot ini ditarik berwarna merah dan biru pada Gambar 2. Yang ketiga berbobot hijau, dapat menyeimbangkan kekuatan yang dihasilkan dari dua lainnya dan menjaga sistem tetap seimbang.

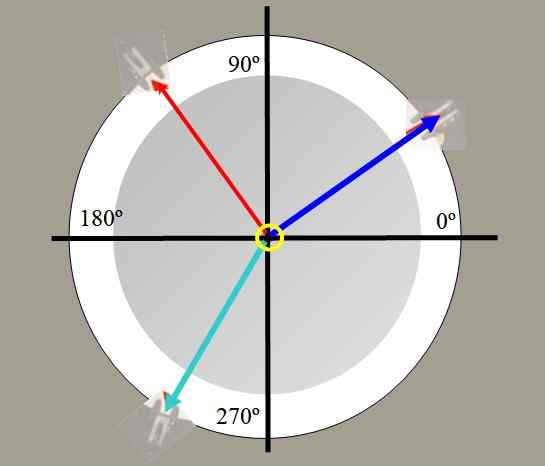Gambar 2. Lihat dari atas tabel Forces. Sumber: Made sendiri.

Dengan tabel kekuatan Anda dapat memverifikasi karakter vektor kekuatan, membusuk kekuatan, menemukan kekuatan penyeimbang dan memverifikasi teorema Lamy:

Dapat melayani Anda: matahari

Jika sebuah Tubuh dalam keseimbangan berkat tiga kekuatan coplanar, bersamaan dan non -kolineal (non -paralel), disebut KE, B Dan C, Hubungan antara kekuatan -kekuatan ini adalah sebagai berikut:

A/ sin α = b/ sen β = c/ sen γ

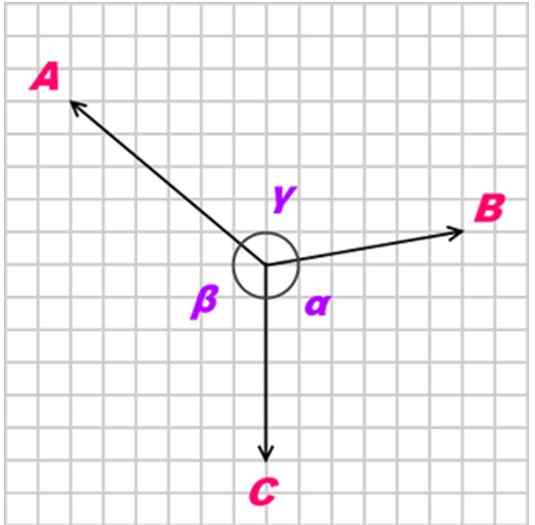Gambar 3. Teorema Lamy berlaku untuk pasukan bersamaan dan coplanar. Sumber: Wikimedia Commons.

Latihan terpecahkan

-Latihan 1

Di tabel gaya pada Gambar 2 berat 225 g (tegangan biru) dan 150 g (tegangan merah) digantung, dengan sudut yang ditunjukkan. Temukan nilai gaya penyeimbang dan sudut yang bentuknya dengan sumbu vertikal.

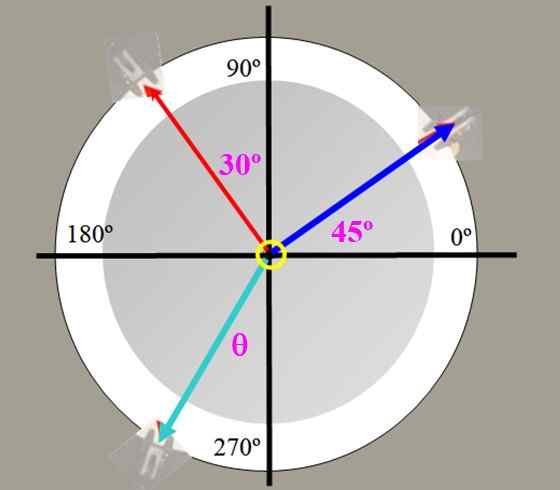Gambar 4. Tabel Pasukan untuk Latihan 1.

Larutan

Masalahnya dapat dikerjakan dengan bobot yang diungkapkan dalam gram (kekuatan). Biarkan hal₁ = 150 gram dan p₂ = 225 gram, masing -masing komponen masing -masing adalah:

P_1x = 225 . cos 45º G = 159.10 g; P_1y = 225 . cos 45º G = 159.10 g

P_2x = -150 . Sen 30º G = -75.00 g; P_{2 dan} = 150 . Cos 30º G = 129.90 g

Berat yang dihasilkan P_R Komponennya secara aljabar menambahkan:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

Berat Balancing P_DAN adalah vektor yang berlawanan P_R:

P_Mantan = -84.10 g

P_Hai = -289.00 g

Besarnya berat penyeimbang dihitung oleh:

P_DAN = (P_Mantan² + P_Hai²)^1/2 = ((-84.10)² + (-289.00)²)^1/2 G = 301 g

Sudut θ dari gambar adalah:

θ = arctg (-84.10 / -289.00) = 16.Ke -2 sehubungan dengan sumbu Dan negatif.

-Latihan 2

Temukan vektor penyeimbang sistem yang ditunjukkan pada gambar, mengetahui bahwa setiap kuadrat berukuran 10 m sisi.

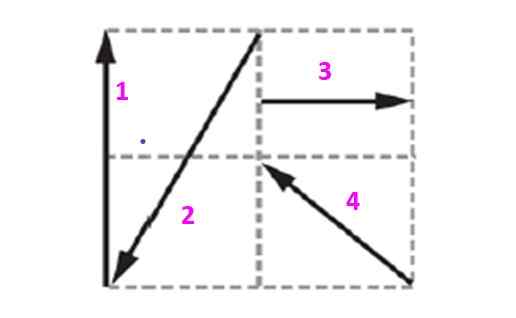Gambar 5. Diagram untuk contoh diselesaikan 2.

Larutan

Vektor yang terkandung dalam kisi ini akan dinyatakan dalam hal unit dan vektor ortogonal yo Dan J yang menentukan pesawat. Vektor 1, yang akan dilambangkan sebagai v₁ Ini memiliki magnitudo 20 m dan diarahkan secara vertikal ke atas. Itu bisa dinyatakan sebagai:

Ini dapat melayani Anda: Perpindahan Panas Radiasi (dengan contoh)

v₁ = 0 yo +dua puluh J M

Dari gambar itu diamati bahwa Vektor 2 adalah:

v₂ = -10 yo - dua puluh J M

Vektor 3 adalah horizontal dan titik dalam alamat positif:

v₃ = 10 yo + 0 J  M

Akhirnya, Vektor 4 cenderung 45 º, karena diagonal kuadrat, oleh karena itu komponennya mengukur sama:

v₄ = -10 yo + 10 J M

Perhatikan bahwa tanda itu -.

Vektor yang dihasilkan diperoleh dengan menambahkan komponen komponen:

v_R = -10 yo + 10 J M

Maka vektor penyeimbang sistem adalah:

v_DAN = 10 yo - 10 J M

Referensi

1. Beardon, t. 2011. Pengantar Vektor. Pulih dari: nrich.Matematika.org.
2. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley. 38-52.
3. Figueroa, d. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika.31-68.
4. Fisik. Modul 8: Vektor. Dipulihkan dari: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mekanika untuk Insinyur. Statis. Edisi ke -6. Perusahaan Editorial Kontinental. 15-53.
6. Vektor kalkulator tambahan. Pulih dari: 1728.org
7. Vektor. Pulih dari: wikibooks.org