Properti, Contoh, Latihan Vektor Gratis

Itu vektor gratis Mereka adalah mereka yang sepenuhnya ditentukan oleh besarnya, arah dan maknanya, tanpa diperlukan untuk menunjukkan titik aplikasi atau asal tertentu.

Karena vektor tak terbatas dapat ditarik dengan cara ini, vektor gratis bukanlah entitas yang unik, tetapi satu set vektor paralel dan identik yang tidak tergantung pada tempat di mana mereka berada.

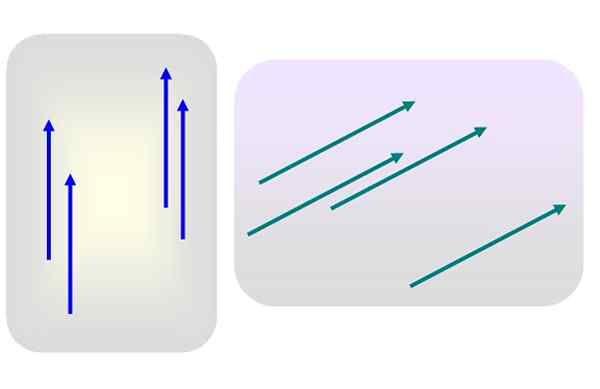
Gambar 1. Berbagai vektor gratis. Sumber: Made sendiri.

Katakanlah ada beberapa vektor magnitudo 3 diarahkan secara vertikal ke atas, atau besarnya 5 dan cenderung ke kanan, seperti pada Gambar 1.

Tidak satu pun dari vektor -vektor ini secara khusus diterapkan pada beberapa titik. Maka salah satu vektor biru atau hijau mewakili kelompok masing -masing, karena karakteristiknya - modul, arah dan indera - tidak dimodifikasi sama sekali ketika mereka dipindahkan ke tempat lain dari pesawat.

Vektor gratis biasanya dilambangkan dalam teks tercetak dengan huruf kecil dan berani, misalnya v. Atau dengan huruf kecil dan panah di atasnya jika itu adalah teks naskah.

[TOC]

 Contoh

Keuntungan yang dimiliki vektor bebas adalah bahwa mereka dapat dipindahkan dengan pesawat atau ruang dan mempertahankan sifatnya, karena setiap perwakilan dari set tersebut sama -sama valid.

Itulah sebabnya dalam fisika dan mekanik sering digunakan. Misalnya, untuk menunjukkan kecepatan linier dari padatan yang bergerak tidak perlu memilih titik tertentu dari objek. Kemudian vektor kecepatan berperilaku seperti vektor bebas.

Contoh lain dari vektor gratis adalah sepasang kekuatan. A pasangan Ini terdiri dari dua kekuatan dengan besarnya dan arah yang sama, tetapi dari indera yang berlawanan, diterapkan pada titik yang berbeda dari padatan. Efek pasangan bukan untuk mentransfer objek, tetapi menyebabkan rotasi berkat momen diproduksi.

Gambar 2 menunjukkan sepasang gaya yang diterapkan pada roda kemudi. Melalui kekuatan F₁ Dan F₂, Torsi yang memutar roda kemudi di sekitar pusatnya dibuat dan dalam jadwal.

Itu dapat melayani Anda: boron nitride (bn): struktur, sifat, mendapatkan, menggunakan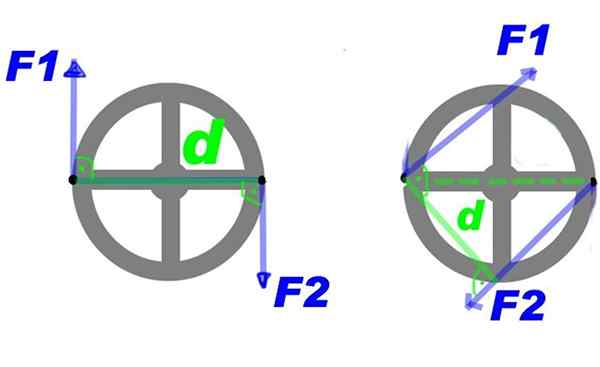 Gambar 2. Beberapa kekuatan yang diterapkan pada setir memberikan giliran skor. Sumber: Bensko [domain publik].

Anda dapat membuat beberapa perubahan pada pasangan dan terus mendapatkan efek rotasi yang sama, misalnya meningkatkan gaya, tetapi mengurangi jarak di antara mereka. Atau mempertahankan kekuatan dan jarak, tetapi oleskan pasangan pada beberapa titik lain pada roda kemudi, yaitu, putar torsi di tengah tengah.

Waktu sepasang kekuatan atau sederhana pasangan, Itu adalah vektor yang modulnya Fd dan tegak lurus terhadap bidang roda tegak lurus. Dalam contoh yang ditunjukkan oleh konvensi, giliran waktu masuk akal.

Properti dan Karakteristik

Berbeda dengan vektor V gratis, vektor AB Dan CD Mereka diperbaiki (lihat Gambar 3), karena mereka telah menentukan titik awal dan titik kedatangan. Tetapi menjadi peralatan satu sama lain, dan pada gilirannya dengan vektor v, Mereka mewakili vektor gratis v.

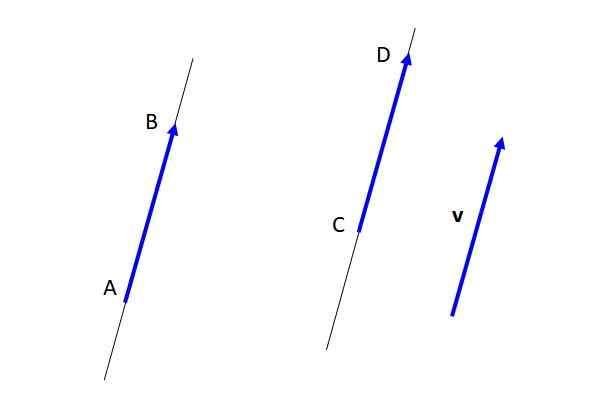Gambar 3. Vektor gratis, peralatan, dan vektor tetap. Sumber: Made sendiri.

Sifat utama vektor gratis adalah sebagai berikut:

-Vektor apa pun AB (Lihat Gambar 2) Seperti yang dinyatakan, mewakili vektor bebas v.

-Modul, arah, dan makna adalah sama di perwakilan vektor gratis. Pada Gambar 2, vektor AB Dan CD Mereka mewakili vektor gratis v Dan mereka adalah peralatan.

-Diberi titik p ruang, selalu mungkin untuk menemukan perwakilan vektor gratis v yang asalnya dalam P dan perwakilan tersebut unik. Ini adalah properti terpenting dari vektor gratis dan yang membuat mereka sangat fleksibel.

Dapat melayani Anda: Eropa (satelit): Karakteristik, komposisi, orbit, gerakan

-Vektor gratis yang dilambangkan dilambangkan sebagai 0 Dan itu adalah himpunan semua vektor yang kurang memiliki besarnya, arah dan makna.

-Jika vektor AB mewakili vektor gratis v, Lalu vektor Ba mewakili vektor gratis -v.

-Notasi akan digunakan V³ untuk menunjuk set semua vektor bebas ruang dan V² Untuk menunjuk semua vektor bebas pesawat.

Latihan terpecahkan

Dengan vektor gratis Anda dapat melakukan operasi berikut:

-Tambahan

-Pengurangan

-Multiplikasi pendakian dengan vektor

-Produk skalar antara dua vektor.

-Produk melintasi antara dua vektor

-Kombinasi linear vektor

Dan lebih banyak lagi.

-Latihan 1

Seorang siswa bermaksud untuk berenang dari titik di pantai dari satu sungai ke sungai lain yang justru di depan. Untuk tidak mencapai apa pun secara langsung dengan kecepatan 6 km / jam, dalam arah tegak lurus, namun arus memiliki kecepatan 4 km / jam yang mengalihkannya.

Hitung kecepatan yang dihasilkan dari perenang dan berapa banyak yang dialihkan oleh arus.

Larutan

Kecepatan perpanjangan perenang adalah jumlah vektor kecepatannya (sehubungan dengan sungai, ditarik secara vertikal) dan kecepatan sungai (ditarik dari kiri ke kanan), yang dilakukan seperti yang ditunjukkan pada gambar di bawah ini:

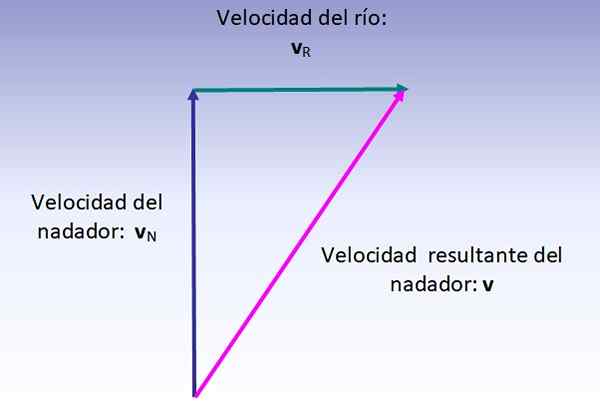
Besarnya kecepatan yang dihasilkan sesuai dengan hipotenuse dari segitiga kanan yang ditunjukkan, oleh karena itu: oleh karena itu:

V = (6² + 4²) ^½ km/h = 7.2 km/jam

Alamat dapat dihitung dengan sudut sehubungan dengan tegak lurus terhadap pantai:

α = arctg (4/6) = 33.7 atau 56.3 tentang pantai.

Latihan 2

Temukan waktu pasangan kekuatan yang ditunjukkan pada gambar:

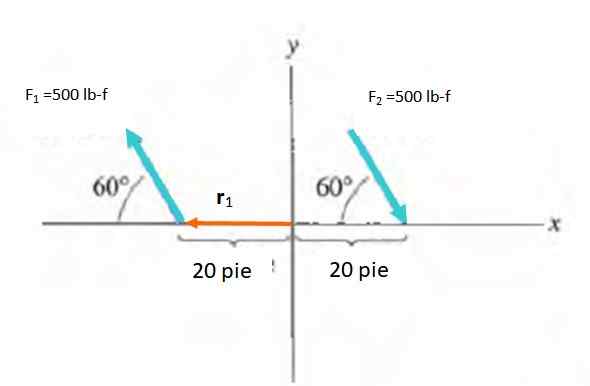
Larutan

Momen ini dihitung oleh:

Dapat melayani Anda: guncangan inelastik: dalam dimensi dan contoh

M = R X F

Unit momen adalah lb-f.kaki. Karena torsi berada di bidang layar, momennya diarahkan tegak lurus, baik ke luar maupun ke dalam.

Karena torsi contoh cenderung mengubah objek yang diterapkannya (yang tidak ditunjukkan pada gambar) dalam jadwal, momen ini dipertimbangkan dengan menunjuk ke dalam layar dan dengan tanda negatif.

Besarnya momen adalah m = f.D.dosa A, berada pada sudut antara gaya dan vektor R. Anda harus memilih titik untuk menghitung momen, yang merupakan vektor gratis. Asal usul sistem referensi dipilih, oleh karena itu R berubah dari O ke titik penerapan masing -masing kekuatan.

M₁ = M₂ = -Fdsen60º = -500 . dua puluh .Sen 60º lb-f . kaki = -8660.3 lb-f . kaki

Momen bersih adalah jumlah m₁ dan m₂: -17329.5 lb-f . kaki.

Referensi

1. Beardon, t. 2011. Pengantar Vektor. Pulih dari: nrich.Matematika.org.
2. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley. 38-52.
3. Figueroa, d. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika.31-68.
4. Fisik. Modul 8: Vektor. Dipulihkan dari: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mekanika untuk Insinyur. Statis. Edisi ke -6. Perusahaan Editorial Kontinental. 15-53.
6. Vektor kalkulator tambahan. Pulih dari: 1728.org
7. Vektor. Pulih dari: itu.Wikibooks.org