Vektor dalam ruang cara grafik, aplikasi, latihan

A vektor di luar angkasa Itu semua diwakili oleh sistem koordinat yang diberikan oleh X, Dan Dan z. Hampir selalu pesawat Xy Itu adalah bidang permukaan horizontal dan sumbu z mewakili tinggi (atau kedalaman).

Sumbu koordinat cartesian yang ditunjukkan pada Gambar 1, membagi ruang menjadi 8 daerah yang disebut Octavers, analog dengan bagaimana sumbu X - Dan Bagilah pesawat menjadi 4 kuadran. Kami kemudian akan memiliki 1 oktan, ocanto ke -2 dan sebagainya.

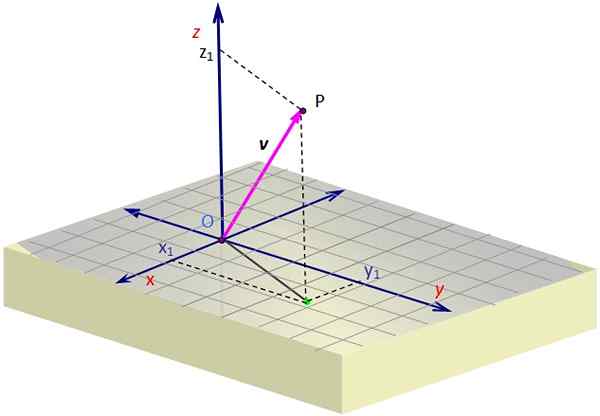
Gambar 1. Vektor di luar angkasa. Sumber: Made sendiri.

Gambar 1 berisi representasi vektor v di ruang. Beberapa perspektif diperlukan untuk menciptakan ilusi tiga dimensi pada bidang layar, yang dicapai dengan menggambar tampilan miring.

Untuk grafik vektor 3D, Anda harus membantu garis putus -putus yang menentukan koordinat proyeksi atau "bayangan" dari grid v Di atas permukaan X-dan. Proyeksi ini dimulai di O dan berakhir di titik hijau.

Sesama Anda harus melanjutkan dengan vertikal ke ketinggian (atau kedalaman) yang diperlukan sesuai dengan nilai z, Sampai Anda sampai di P. Vektor diambil dari O dan berakhir di P, yang dalam contohnya ada di 1st ocant.

[TOC]

Aplikasi

Vektor di ruang angkasa banyak digunakan dalam mekanika dan cabang fisika dan teknik lainnya, karena struktur yang mengelilingi kita membutuhkan geometri dalam tiga dimensi.

Posisi vektor di ruang digunakan untuk memposisikan objek sehubungan dengan titik referensi yang disebut asal SALAH SATU. Oleh karena itu mereka juga merupakan alat yang diperlukan dalam navigasi, tetapi bukan itu saja.

Dapat melayani Anda: Gelombang Elektromagnetik: Teori, Jenis, Karakteristik Maxwell

Kekuatan yang bekerja pada struktur seperti baut, penyangga, kabel, struts dan lainnya adalah sifat vektor dan berorientasi pada ruang angkasa. Untuk mengetahui efeknya, perlu mengetahui alamat Anda (dan juga poin aplikasi Anda).

Dan seringkali arah suatu gaya diketahui oleh dua titik di ruang yang termasuk dalam garis aksinya. Dengan cara ini kekuatannya adalah:

F = F atau

Di mana f adalah besarnya atau modul gaya dan atau Ini adalah vektor unit (modul 1) yang diarahkan di sepanjang garis aksi F. 

Notasi dan representasi vektor 3D

Sebelum menyelesaikan beberapa contoh, notasi vektor 3D akan ditinjau secara singkat.

Dalam contoh Gambar 1, Vektor V, yang titik asalnya bertepatan dengan asal atau dan yang endingnya adalah titik P, memiliki koordinat X Dan z positif, saat koordinat Dan Itu negatif. Koordinat ini adalah: X₁, Dan₁, z₁, yang justru koordinat p.

Jadi jika kita memiliki vektor yang terkait dengan asal, yaitu, yang titik awalnya bertepatan dengan O, sangat mudah untuk menunjukkan koordinatnya, yang akan menjadi titik ekstrem atau p. Untuk membedakan antara titik dan vektor, kami akan menggunakan untuk huruf dan kurung berani terbaru, seperti ini:

v = < x₁, Dan₁, z₁ >

Sementara titik P dilambangkan dengan tanda kurung:

P = (x₁, Dan₁, z₁)

Representasi lain memanfaatkan vektor unit yo, J Dan k yang menentukan tiga arah ruang dalam sumbu X, Dan Dan z masing -masing.

Vektor -vektor ini saling tegak lurus dan membentuk a Basis Ortonormal (Lihat Gambar 2). Ini berarti bahwa vektor 3D dapat ditulis dalam hal mereka sebagai:

Dapat melayani Anda: Gerakan bergelombang: Karakteristik, jenis gelombang, contoh

v = v_X yo + v_Dan J + v_z k

Direktur Vektor Sudut dan Cosenos

Gambar 2 juga menunjukkan sudut sutradara γ₁, γ₂ dan γ₃ dari vektor v masing -masing dengan kapak X, Dan Dan z. Mengetahui sudut -sudut ini dan besarnya vektor, ini sepenuhnya ditentukan. Selain itu, cosinus dari direktur memenuhi hubungan berikut:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

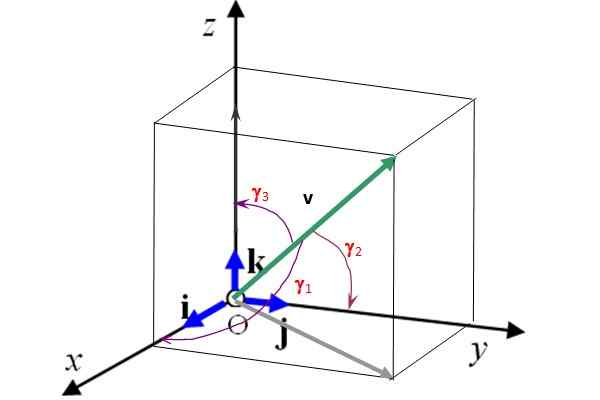Gambar 2. Vektor kesatuan i, j dan k menentukan 3 arah preferensial ruang. Sumber: Made sendiri.

Latihan terpecahkan

-Latihan 1

Pada Gambar 2 sudut γ₁, γ₂ dan γ₃ dari vektor v Modul 50 bentuk dengan sumbu koordinat masing -masing: 75.0º, 60.0º dan 34.3. Temukan komponen cartesian dari vektor ini dan mewakili itu dalam hal vektor unit yo, J Dan k.

Larutan

Proyeksi vektor v pada poros X adalah v_X = 50 . Cos 75º = 12.941. Demikian pula proyeksi v pada poros Dan adalah v_Dan = 50 cos 60 º = 25 dan akhirnya pada sumbu z adalah v_z = 50. cos 34.3 = 41.3. Sekarang v dapat dinyatakan sebagai:

v = 12.9 yo + 25.0 J + 41.3 k

-Latihan 2 

Temukan ketegangan di masing -masing kabel yang menahan ember gambar yang ada dalam kesetimbangan, jika beratnya adalah 30 N.

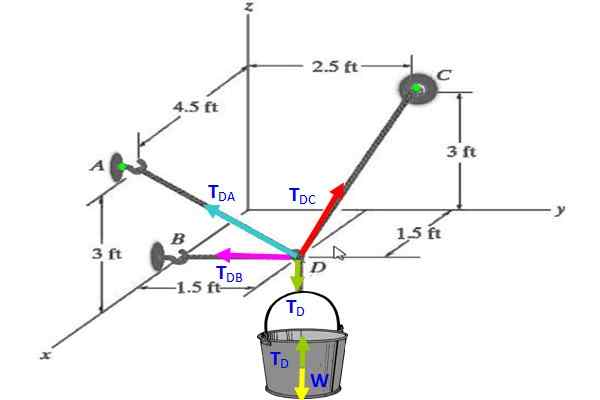Gambar 3. Diagram Ketegangan untuk Latihan 2.

Larutan

Pada ember, diagram tubuh bebas menunjukkan itu T_D (hijau) mengkompensasi berat badan W (kuning), oleh karena itu t_D = W = 30 n.

Di simpul, vektor T_D  Diarahkan secara vertikal ke bawah, lalu:

T_D = 30 (-k) N.

Untuk menetapkan ketegangan yang tersisa, Anda harus mengikuti langkah -langkah berikut:

Langkah 1: Temukan koordinat semua poin

A = (4.5; 0; 3) (A ada di bidang dinding X-z)

B = (1.5; 0; 0) (B ada pada sumbu x)

Dapat melayani Anda: alamat (fisik)

C = (0, 2.5, 3) (C ada di bidang dinding dan z)

D = (1.5; 1.5; 0) (D berada di bidang horizontal  X-dan)

Langkah 2: Temukan vektor di setiap arah dengan mengurangi koordinat akhir dan awal

Memberi =

Dc =

Db =

Langkah 3: Hitung modul dan vektor unit

Vektor unit diperoleh dengan ekspresi: atau = R / r, dengan R (dalam tebal) menjadi vektor dan r (tanpa tebal) modul vektor tersebut.

Da = (3² + (-1.5)² + 3²)^½ = 4.5; DC = ((-1.5) ² + 1² + 3²)^½ = 3.5

atau_Memberi = 4.5 =

atau_Dc = 3.5 =

atau_Db =

atau_D =

Langkah 4: Ekspresikan semua ketegangan sebagai vektor

T_Memberi = T_Memberi atau_Memberi = T_Memberi

T_Dc = T_Dc atau_{Dc =}  T_Dc

T_Db = T_Db atau_Db = T_Db

 T_D = 30

Langkah 5: Terapkan kondisi keseimbangan statis dan selesaikan sistem persamaan

Akhirnya, kondisi keseimbangan statis diterapkan pada ember, sehingga jumlah vektor dari semua kekuatan pada simpul batal:

T_Memberi + T_Dc + T_Db + T_D = 0

Karena ketegangan ada di ruang angkasa, itu akan mengarah ke sistem tiga persamaan untuk setiap komponen (X, dan dan z) ketegangan.

0.67 t_Memberi -0.43 t_Dc + 0 t_Db = 0

-0.33 t_Memberi + 0.29 t_Dc - T_Db = 0

0.67 t_Memberi + 0.86 t_Dc +0 t_Db - 30 = 0

Solusinya adalah: t_Memberi = 14.9 n; T_Memberi = 23.3 n; T_Db = 1.82 n

Referensi

1. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley. 38-52.
2. Figueroa, d. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika.31-68.
3. Fisik. Modul 8: Vektor. Dipulihkan dari: FRTL.Utn.Edu.ar
4. Hibbeler, R. 2006. Mekanika untuk Insinyur. Statis. Edisi ke -6. Perusahaan Editorial Kontinental. 15-53.
5. Vektor kalkulator tambahan. Pulih dari: 1728.org