Fisik

Definisi, Notasi, Latihan Equiposent Vektor

Definisi, Notasi, Latihan Equiposent Vektor

Dua atau lebih Vektor adalah peralatan Jika mereka memiliki modul yang sama, arah yang sama dan indera yang sama, bahkan ketika titik asal mereka berbeda. Ingatlah bahwa karakteristik vektor justru: asal, modul, arah dan indera. 

Vektor diwakili oleh segmen berorientasi atau panah. Gambar 1 menunjukkan representasi beberapa vektor di pesawat, beberapa di antaranya adalah peralatan sesuai dengan definisi yang awalnya diberikan.

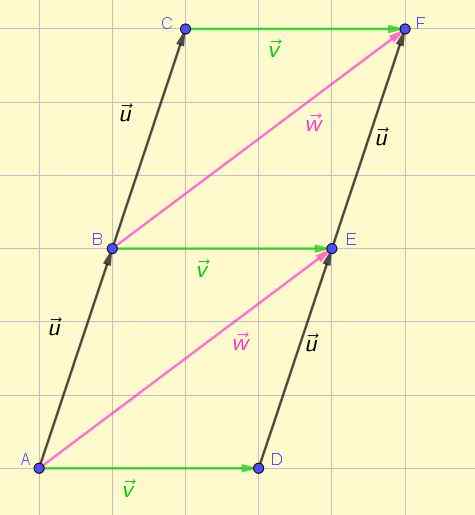Gambar 1. Vektor peralatan dan non -peralatan. Sumber: Made sendiri.

Dari pandangan pertama adalah mungkin untuk menghargai bahwa tiga vektor hijau memiliki ukuran yang sama, arah yang sama dan pengertian yang sama. Hal yang sama dapat ditegaskan tentang dua vektor merah muda dan empat vektor hitam.

Sejumlah besar alam memiliki perilaku vektor, seperti kasus kecepatan, akselerasi dan kekuatan, untuk menyebutkan hanya beberapa. Oleh karena itu pentingnya mengkarakterisasi mereka dengan benar.

[TOC]

Notasi untuk vektor dan peralatan

Untuk membedakan jumlah vektor dari jumlah skalar, huruf tipe hitam atau panah pada huruf sering digunakan. Saat bekerja dengan vektor tangan, di buku catatan, perlu membedakannya dengan panah dan ketika media cetak digunakan, yang tebal digunakan.

Vektor dapat ditolak menunjukkan titik awal atau asal mereka dan titik kedatangan mereka. Misalnya AB, Bc, DARI Dan EF Namun, dari Gambar 1 adalah vektor AB, Bc, DARI Dan EF Mereka adalah jumlah atau angka skalar yang menunjukkan besarnya, modul atau ukuran vektor masing -masing.

Untuk menunjukkan bahwa dua vektor adalah peralatan, simbol digunakan "∼ ". Dengan notasi ini, pada gambar kita dapat menunjukkan vektor berikut yang merupakan peralatan satu sama lain:

Dapat melayani Anda: energi kinetik: karakteristik, jenis, contoh, latihan

AB∼BCSDE TEF 

Mereka semua memiliki besarnya, arah, dan makna yang sama. Oleh karena itu mematuhi peraturan yang ditunjukkan di atas.

Vektor bebas, geser dan berlawanan

Salah satu vektor dalam gambar (misalnya AB) adalah perwakilan dari set semua vektor tetap tetap. Set tak terbatas ini mendefinisikan kelas vektor gratis atau.

atau = Ab, bc, from, ef, ..

Notasi alternatif adalah sebagai berikut:

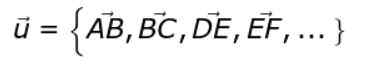
Jika tebal atau panah tidak ditempatkan di atas atau, Kami ingin merujuk ke modul vektor atau.

Vektor gratis tidak diterapkan pada titik tertentu.

Untuk bagian mereka Vektor geser Mereka adalah peralatan peralatan ke vektor yang diberikan, tetapi titik penerapannya harus terkandung dalam jalur aksi vektor.

Dan vektor yang berlawanan Mereka adalah vektor yang memiliki besarnya dan arah yang sama tetapi indera yang berlawanan, meskipun dalam teks bahasa Inggris mereka disebut Alamat yang berlawanan karena alamat juga menunjukkan artinya. Vektor yang berlawanan bukanlah peralatan.

Latihan

-Latihan 1

Vektor lain mana yang ditunjukkan pada Gambar 1 adalah peralatan satu sama lain?

Larutan

Terlepas dari yang sudah ditunjukkan pada bagian sebelumnya, diamati dari Gambar 1 itu IKLAN, Menjadi Dan Ec Mereka juga melengkapi vektor satu sama lain:

AD ∼ menjadi ∼ CE 

Salah satu dari mereka adalah perwakilan dari kelas vektor gratis v.

Vektor juga merupakan peralatan di antara mereka sendiri AE Dan Bf :

AE ∼ Bf 

Siapa perwakilan kelas W.

-Latihan 2

Poin A, B dan C berada di pesawat XY Cartesian dan koordinatnya adalah:

Dapat melayani Anda: Gas Ideal: Model, Perilaku, Contoh

A = (-4.1), b = (-1.4) dan c = (-4, -3)

Temukan koordinat titik keempat D sehingga vektor AB Dan CD Menjadi peralatan.

Larutan 

Sehingga CD menjadi peralatan AB harus memiliki modul yang sama dan arah yang sama dengan AB .

Modul AB Kotak adalah:

|AB|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D Koordinat tidak diketahui dengan apa yang bisa kita katakan: d = (x, y)

Lalu: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

AS |AB| = |CD| Itu adalah salah satu syarat untuk AB Dan CD Menjadi peralatan yang Anda miliki:

(x + 4)^2 + (y + 3)^2 = 18

Karena ada dua yang tidak diketahui, persamaan lain diperlukan, yang dapat dicapai dari kondisi bahwa AB Dan CD menjadi paralel dan dalam arti yang sama.

Vektor AB Slope

Kemiringan vektor AB menunjukkan alamat Anda:

Tertunda ab = (4 -1)/(-1 -( -4)) = 3/3 = 1

Menunjukkan bahwa vektor AB 45º bentuk dengan sumbu x.

Kemiringan Vektor CD

Kemiringan CD Itu dihitung dengan cara yang sama:

Tertunda cd = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Mencocokkan hasil ini dengan kemiringan AB Anda memiliki persamaan berikut:

Y + 3 = x + 4 

Yang berarti y = x + 1.

Jika hasil ini diganti dalam persamaan kesetaraan modul, itu adalah:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Menyederhanakan adalah:

2 (x+4)^2 = 18, 

Yang setara dengan:

(x+4)^2 = 9

Yaitu x+4 = 3 yang menyiratkan bahwa x = -1. Sehingga koordinat D adalah (-1, 0).

memeriksa

Komponen vektor AB Mereka adalah (-1-(-4); 4 -1) = (3; 3)

Dapat melayani Anda: Teorema THévenin: Apa yang terdiri dari, aplikasi, dan contoh

dan orang -orang dari vektor CD mereka adalah (-1-(-4)); 0 -(-3)) = (3; 3)

Yang berarti bahwa vektor adalah peralatan. Jika dua vektor memiliki komponen cartesian yang sama memiliki modul dan arah yang sama, oleh karena itu mereka adalah peralatan.

-Latihan 3

Vektor gratis atau memiliki besarnya 5 dan alamat 143.1301º.

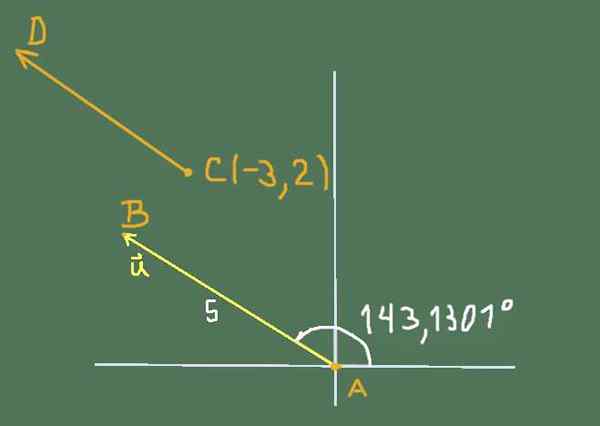
Temukan komponen cartesian -nya dan tentukan koordinat titik B dan C mengetahui bahwa vektor tetap AB dan CD adalah peralatan. Koordinat A adalah (0, 0) dan koordinat titik C adalah (-3,2).

Larutan 

Situasi yang diusulkan oleh latihan dapat diwakili oleh gambar berikut:

Gambar 2. Diagram untuk Resolusi Latihan 3. Sumber: Made sendiri.

Komponen Cartesian dari atau adalah

atau = (5*cos (143.1301º); 5*sin (143.1301º))) 

Membuat perhitungan tetap:

atau = (-4; 3) 

Koordinat B tidak diketahui, jadi kami akan menempatkan B (x, y)

Koordinat Vektor AB Mereka adalah (x-0; y-0), tetapi karena peralatan dengan Anda harus dipenuhi kesetaraan komponen, oleh karena itu disimpulkan bahwa koordinat B adalah (-4, 3).

Demikian pula koordinat vektor CD Mereka adalah (x-(-3)); (dan - 2) Itu pasti peralatan u, latau itu mengarah ke:

 x + 3 = -4 dan y -2 = 3

Maka koordinat titik D akan menjadi (-7, 5).

Referensi

  1. Perhitungan.Dc. Vektor tetap. Vektor gratis. Pulih dari: perhitungan.Dc
  2. 2d Descartes. Memperbaiki vektor dan vektor bebas pesawat. Diperoleh dari: sumber daya.pendidikan.adalah
  3. Proyek Guao. Vektor peralatan. Pulih dari: guao.org
  4. Resnick, r., Krane, k. (2001). Fisika (dalam bahasa Inggris). New York: John Wiley & Sons.
  5. Serway, r.; Jewett, John W. (2004). Fisika untuk Ilmuwan dan Insinyur (dalam bahasa Inggris) (Edisi ke -6). Brooks/Cole.
  6. Tupler, Paul A. (2000). Fisika untuk Sains dan Teknologi. Volume I. Barcelona: ed. Saya terbalik.
  7. Weisstein, e. "Vektor". Di Weisstein, Eric W. MathWorld (dalam bahasa Inggris). Penelitian Wolfram.