Perhitungan vektor yang dihasilkan, contoh, latihan

Dia vektor yang dihasilkan Itu adalah yang diperoleh dengan operasi dengan vektor yang hasilnya juga merupakan vektor. Biasanya operasi ini adalah jumlah dari dua atau lebih vektor, yang melaluinya vektor diperoleh yang efeknya setara.

Dengan cara ini vektor seperti kecepatan, akselerasi atau gaya diperoleh hasilnya. Misalnya ketika beberapa kekuatan bertindak pada tubuh F₁, F₂, F₃,.. . Jumlah vektor dari semua kekuatan ini setara dengan gaya bersih (hasil yang dihasilkan), yang secara matematis mengekspresikan dirinya:

F₁ + F₂ + F₃ +… = F_R  salah satu F_N

Gambar 1. Bobot salju didistribusikan di atas langit -langit dan aksinya dapat diganti dengan gaya tunggal yang diterapkan di tempat yang sesuai. Sumber: Pixabay.

Vektor yang dihasilkan, apakah itu kekuatan atau besarnya vektor lainnya, menerapkan aturan jumlah vektor. Karena vektor memiliki arah dan akal selain nilai numerik, tidak cukup untuk menambahkan modul untuk memiliki vektor yang dihasilkan.

Ini benar hanya dalam kasus di mana vektor yang terlibat berada dalam arah yang sama (lihat contoh). Kalau tidak perlu menggunakan metode jumlah vektor, yang, tergantung pada kasusnya, dapat berupa geometris atau analitik.

[TOC]

Contoh

Metode geometris untuk menemukan vektor yang dihasilkan adalah metode poligon dan metode jajaran genjang.

Adapun metode analitik adalah metode komponen, yang melaluinya vektor yang dihasilkan dari sistem vektor dapat ditemukan, selama kami memiliki komponen cartesiannya.

Metode geometris untuk menambahkan dua vektor

Misalkan vektor atau Dan v (Kami menunjukkan mereka dengan huruf tebal untuk membedakan mereka dari skalar). Pada Gambar 2) kami memiliki mereka berada di pesawat. Pada Gambar 2 b) telah pindah ke Vektor V sedemikian rupa sehingga asalnya bertepatan dengan akhir atau. Vektor yang dihasilkan berasal dari asal yang pertama (atau) ke ujung terakhir (v):

Itu dapat melayani Anda: kompresibilitas: padatan, cairan, gas, contoh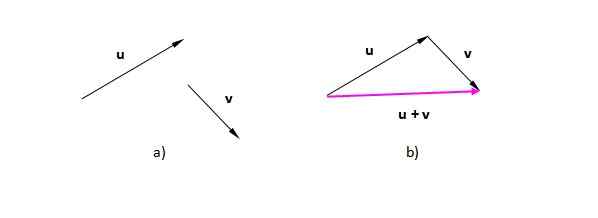 Gambar 2. Vektor yang dihasilkan dari jumlah grafik vektor. Sumber: Made sendiri.

Angka yang menghasilkan kasus ini adalah segitiga (segitiga adalah poligon 3 -sided). Jika kita memiliki dua vektor dalam arah yang sama, prosedurnya sama: tempatkan salah satu vektor demi satu dan menggambar satu yang berasal dari asal atau ekor yang pertama ke ujung atau ujung yang terakhir.

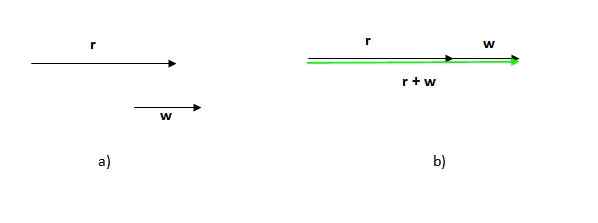
Perhatikan bahwa urutan prosedur ini dibuat tidak masalah, karena jumlah vektor adalah komutatif.

Perhatikan juga bahwa dalam hal ini modul (Panjang atau ukuran) dari vektor yang dihasilkan adalah jumlah modul vektor tambahan, tidak seperti kasus sebelumnya, di mana modul vektor yang dihasilkan kurang dari jumlah modul peserta.

Metode jajaran genjang

Metode ini sangat tepat ketika Anda perlu menambahkan dua vektor yang titik asalnya setuju, dengan asal sistem koordinat x-y. Misalkan ini adalah kasus vektor kami atau Dan v (Gambar 3):

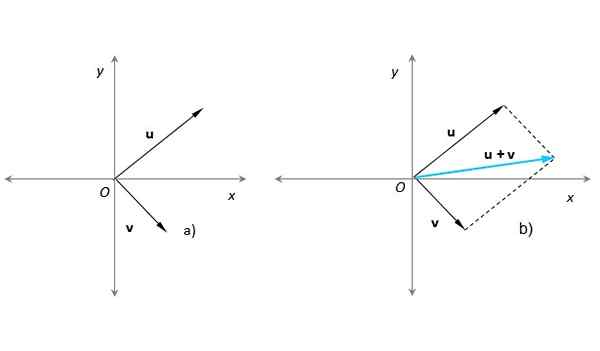Gambar 3. Jumlah dua vektor dengan menggunakan metode jajaran genjang dengan vektor yang dihasilkan dengan warna biru pirus. Sumber: Made sendiri.

Pada Gambar 3b) jajaran genjang telah dibangun dengan bantuan garis putus -putus paralel atau sudah v. Vektor yang dihasilkan berawal dari O dan ujungnya pada titik di mana garis putus -putus berpotongan. Prosedur ini sepenuhnya setara dengan yang dijelaskan di bagian sebelumnya.

Latihan

-Latihan 1

Mengingat vektor berikut, temukan vektor yang dihasilkan menggunakan metode poligonal.

Itu bisa melayani Anda: refleksi cahaya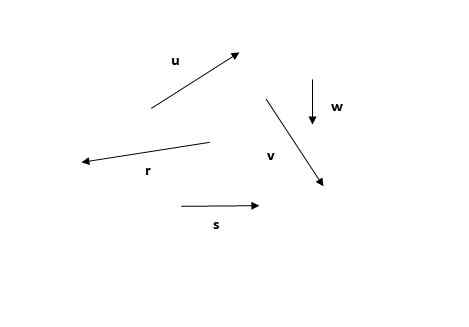 Gambar 4. Vektor untuk menemukan hasilnya melalui metode poligonal. Latihan 1. Sumber: Made sendiri.

Larutan

Metode poligonal adalah yang pertama dari metode yang terlihat. Ingatlah bahwa jumlah vektor adalah komutatif (urutan penambahan tidak mengubah jumlah), sehingga Anda dapat mulai dengan salah satu vektor, misalnya atau (Gambar 5a) atau R (Gambar 5b):

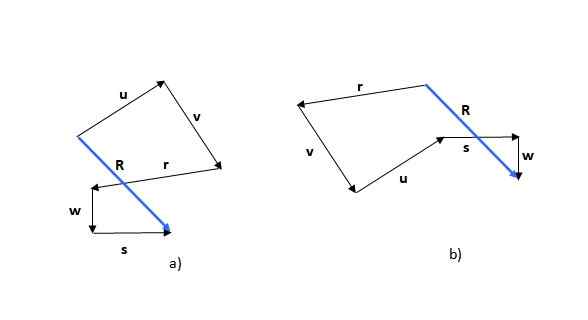Gambar 5. Jumlah vektor melalui metode poligonal. Sumber: Made sendiri.

Gambar yang diperoleh adalah poligon dan vektor yang dihasilkan (berwarna biru) disebut R. Jika Anda mulai dengan vektor lain, gambar yang terbentuk bisa berbeda, seperti yang dapat dilihat pada contoh, tetapi vektor yang dihasilkan adalah sama.

Latihan 2

Pada gambar berikut diketahui bahwa modul vektor atau Dan v masing -masing adalah u = 3 unit sewenang -wenang dan v = 1.8 unit sewenang -wenang. Sudut itu atau Bentuk dengan sumbu x positif adalah 45 º, sedangkan v bentuk 60 º dengan sumbu y, seperti yang terlihat pada gambar. Temukan vektor, besarnya, dan arah yang dihasilkan.

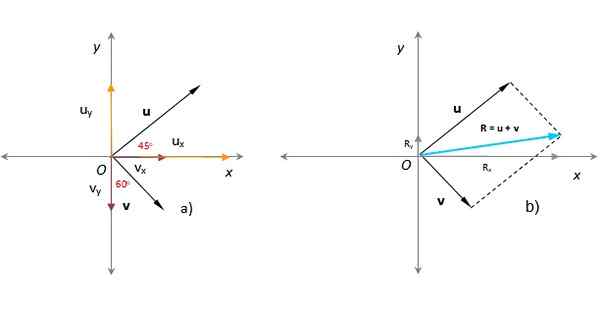
Larutan

Di bagian sebelumnya, vektor yang dihasilkan ditemukan menerapkan metode jajaran genjang (dalam pirus dalam gambar).

Cara sederhana untuk menemukan vektor yang dihasilkan secara analitik adalah dengan mengekspresikan vektor yang menambahkan dalam hal komponen cartesian mereka, yang merupakan tugas yang mudah ketika modul dan sudut diketahui, seperti vektor dari contoh ini:

atau_X = u . cos 45º = 3 x cos 45 º = 2.12; atau_Dan = u . sin 45 º = 3x sen 45º = 2.12

v_X = v . Sen 60º = 1.8 x sen 60 º = 1.56; v_Dan = -V . cos 60 º = -1.8 x cos 60º = - 0.9

Dapat melayani Anda: gerakan pendular

Vektor atau Dan v Mereka adalah vektor milik pesawat, memiliki kedua komponen masing -masing. Vektor U berada di kuadran pertama dan komponennya positif, sedangkan vektor V berada di kuadran keempat; Komponen X -nya positif, tetapi proyeksi pada sumbu vertikal jatuh ke dalam sumbu dan negatif.

Perhitungan komponen Cartesian dari vektor yang dihasilkan

Vektor yang dihasilkan menambahkan secara aljabar komponen masing -masing x dan y, untuk mendapatkan komponen kartesia:

R_X = 2.12 + 1.56 = 3.68

R_Dan = 2.12 + (-0.9) = 1.22

Setelah komponen cartesian ditentukan dan vektor diketahui sepenuhnya. Vektor yang dihasilkan dapat diekspresikan dengan notasi dalam tanda kurung persegi (kurung):

R = unit sewenang -wenang

Notasi braket digunakan untuk membedakan vektor dari titik di pesawat (atau di ruang). Cara lain untuk mengekspresikan vektor yang dihasilkan dengan cara analitik adalah melalui penggunaan vektor unit yo dan J di pesawat (yo, J Dan k di ruang):

R = 3.68 yo + 1.22 J unit sewenang -wenang

Karena kedua komponen vektor yang dihasilkan positif, vektor R Itu milik kuadran pertama, yang sudah terlihat secara grafis.

Besarnya dan arah vektor yang dihasilkan

Dikenal dengan komponen Cartesian, besarnya R dihitung melalui teorema Pythagoras, karena vektor yang dihasilkan R, di sebelah komponennya r_X dan r_Dan Mereka membentuk segitiga siku -siku:

Besarnya atau modul: r = (3.68² + 1.22²)^½ = 3.88

Alamat q Mengambil sumbu x positif sebagai referensi: q = arcan (r_Dan / R_X) = arctg (1.22/3.68) = 18.3

Referensi

1. Menambahkan vektor dan aturan. Pulih dari: newt.Phys.UNSW.Edu.Au
2. Figueroa, d. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika.31-68.
3. Fisik. Modul 8: Vektor. Dipulihkan dari: FRTL.Utn.Edu.ar
4. Hibbeler, R. 2006. Mekanika untuk Insinyur. Statis. Edisi ke -6. Perusahaan Editorial Kontinental. 15-53.
5. Vektor kalkulator tambahan. Pulih dari: www.1728.org