Fisik

Definisi kecepatan sudut, rumus, perhitungan dan latihan

Definisi kecepatan sudut, rumus, perhitungan dan latihan

Itu Kecepatan sudut Ini adalah ukuran kecepatan rotasi dan didefinisikan sebagai sudut yang memutar vektor posisi objek yang berputar, per satuan waktu. Ini adalah besarnya yang menggambarkan dengan sangat baik pergerakan banyak objek yang terus -menerus berbalik ke mana -mana: CD, roda mobil, mesin, bumi dan banyak lagi.

Skema "London Eye" dapat dilihat pada gambar berikut. Itu mewakili pergerakan penumpang yang diwakili oleh titik P, yang mengikuti lintasan melingkar, yang disebut C:

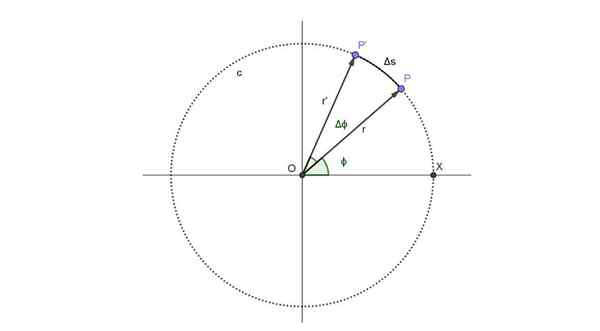Representasi skematis dari lintasan melingkar yang mengikuti penumpang "London Eye". Sumber: Made sendiri.

Penumpang menempati posisi P pada T instan dan posisi sudut yang sesuai dengan momen itu adalah ϕ.

Dari saat periode waktu berlalu. Pada periode itu posisi baru penumpang tepat waktu adalah P 'dan posisi sudut telah meningkatkan sudut Δϕ.

[TOC]

Bagaimana kecepatan sudut dihitung ?

Untuk magnitudo rotasi, huruf -huruf Yunani banyak digunakan, untuk membedakannya dari magnitudo linier. Jadi pada awalnya kecepatan sudut rata -rata Ω ditentukanM Saat sudut berjalan dalam periode waktu tertentu.

Maka hasil bagi Δϕ/Δt akan mewakili kecepatan sudut rata -rata ΩM Di antara momen t dan t+Δt.

Jika Anda ingin menghitung Kecepatan sudut Tepat pada saat itu, maka hasil bagi Δϕ/Δt harus dihitung ketika Δt ➡0:

 Unit ukuran kecepatan sudut adalah rad/s.

Hubungan antara kecepatan linier dan sudut

Kecepatan linier v, Ini adalah hasil bagi antara jarak yang ditempuh dan periode waktu yang digunakan untuk menempuhnya.

Pada gambar di atas, rute busur adalah ΔS. Tetapi busur itu sebanding dengan sudut yang ditempuh dan jari -jari, memenuhi hubungan berikut, yang valid selama Δϕ diukur dalam radian:

Dapat melayani Anda: Metode jajaran genjang: contoh, latihan terpecahkan

ΔS = r ・ Δϕ

Jika kita membagi ekspresi sebelumnya antara periode waktu Δt dan mengambil batas ketika Δt ➡0, kita akan mendapatkan:

v = r ・ Ω

Gerakan rotasi seragam

Foto itu adalah "London Eye" yang terkenal, roda berputar tinggi 135 m yang berputar perlahan, sehingga orang dapat naik kabin di pangkalan mereka dan menikmati lanskap London. Sumber: Pixabay.

Gerakan rotasi seragam jika setiap saat diamati, sudut yang ditempuh adalah sama dalam periode waktu yang sama.

Jika rotasi seragam, maka kecepatan sudut kapan saja bertepatan dengan kecepatan sudut rata -rata.

Dalam gerakan rotasi yang seragam waktu di mana belokan lengkap disebut periode dan menunjukkan dengan t.

Selain itu, ketika sudut diputar, 2π (setara dengan 360º). Itulah sebabnya dalam rotasi yang seragam kecepatan sudut Ω terkait dengan periode t, dengan menggunakan rumus berikut:

Frekuensi didefinisikan F dari rotasi yang seragam seperti hasil bagi antara jumlah belokan dan waktu yang dihabiskan untuk bepergian. Saat saya kembali bepergian dalam waktu t (periode) memiliki hubungan berikut:

F = 1/t

Dengan kata lain, dalam rotasi yang seragam, kecepatan sudut terkait dengan frekuensi dengan:

Ω = 2π ・ f

Latihan kecepatan sudut terpecahkan

Latihan 1

Kabin roda berputar besar yang dikenal sebagai "Mata London"Mereka bergerak perlahan. Kecepatan kabin adalah 26 cm/s dan roda berdiameter 135 m.

Dengan data ini Hitung:

Dapat melayani Anda: matahari

i) kecepatan sudut roda

ii) frekuensi rotasi

iii) waktu yang membutuhkan kabin untuk berbalik.

Jawaban:

Yo) Kecepatan V dalam m/s adalah: v = 26 cm/s = 0,26 m/s.

Radio adalah setengah dari diameter: r = (135 m) / 2 = 67,5 m

v = r ・ Ω => ω = v/r = (0,26 m/s)/(67,5 m) = 0,00385 rad/s

Ii) Ω = 2π ・ f => f = Ω / 2π = (0,00385 rad / s) / (2π rad) = 6.13 x 10-4 belokan/s

F = 6.13 x 10^-4 Turn/S = 0.0368 Turn/Min = 2.21 Turn/Hour.

AKU AKU AKU) T = 1 / f = 1/21 Turn / jam = 0.45311 Waktu = 27 menit 11 detik

Latihan 2

Mobil mainan bergerak di trek melingkar 2m radius. Pada 0 s posisi sudutnya adalah 0 rad, tetapi setelah beberapa waktu, posisi sudut diberikan oleh:

φ (t) = 2 ・ t 

Menentukan:

i) kecepatan sudut 

ii) Kecepatan linier kapan saja.

Jawaban:

Yo) Kecepatan sudut adalah turunan dari posisi sudut: Ω = φ '(t) = 2.

Dengan kata lain.

Ii) Kecepatan linier mobil adalah: V = r ・ ω = 2 m ・ 2 rad/s = 4 m/s = 14,4 km/jam

Latihan 3

Mobil yang sama dari latihan sebelumnya mulai berhenti. Posisi sudutnya sebagai fungsi waktu diberikan oleh ekspresi berikut:

φ (t) = 2 ・ t - 0,5 ・ t2 

Menentukan:

i) Kecepatan sudut kapan saja

ii) Kecepatan linier kapan saja

iii) waktu yang Anda ambil untuk berhenti dari saat Anda mulai melambat

iv) Sudutnya bepergian 

v) Di kejauhan ditempuh

Jawaban:

Yo) Kecepatan sudut adalah turunan dari posisi sudut: Ω = φ '(t)

Ω (t) = φ '(t) = (2 ・ t - 0,5 ・ t2) '= 2 - t

Ii) Kecepatan linear mobil kapan saja diberikan oleh:

v (t) = r ・ Ω (t) = 2 ・ (2 - t) = 4 - 2 t

Dapat melayani Anda: kecepatan relatif: konsep, contoh, latihan

AKU AKU AKU) Waktu yang berlangsung saat di mana ia mulai melambat.

v (t) = 4 - 2 t = 0 => t = 2

Artinya berhenti 2 detik setelah mulai berhenti.

Iv) Pada periode 2s, dari saat itu mulai berhenti sampai sudut yang diberikan oleh φ (2) dilalui:

φ (2) = 2 ・ 2 - 0,5 ・ 2^2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 derajat

V) Dalam rentang 2 S dipahami karena mulai berhenti sampai berhenti jarak yang diberikan oleh:

S = r ・ φ = 2m ・ 2 rad = 4 m

Latihan 4

Roda mobil berdiameter 80 cm. Jika mobil bergerak 100 km/jam. Temukan: i) Kecepatan sudut rotasi roda, ii) Frekuensi rotasi roda, iii) Jumlah putaran yang diberikan roda dalam rute 1 jam.

Jawaban:

Yo) Pertama -tama kita akan mengubah kecepatan mobil km/jam m/s

V = 100 km / jam = (100/3.6) m/s = 27,78 m/s

Kecepatan sudut rotasi roda diberikan oleh:

Ω = v/r = (27,78 m/s)/(0,4 m) = 69,44 rad/s

Ii) Frekuensi rotasi roda diberikan oleh:

F = ω / 2π = (69.44 rad / s) / (2π rad) = 11.05 putaran / s

Frekuensi rotasi biasanya dinyatakan dalam revolusi per menit r.P.M.

F = 11.05 Turn/S = 11.05 Turn/(1/60) Min = 663.15 R.P.M

AKU AKU AKU)  Jumlah putaran yang diberikan roda dalam rute 1 jam, dihitung mengetahui bahwa 1 jam = 60 menit dan bahwa frekuensinya adalah jumlah belokan N dibagi dengan waktu di mana N diberikan.

F = n / t => n = f ・ t = 663.15 (belokan / mnt) x 60 mnt = 39788.7 Turn.

Referensi

  1. Giancoli, d. Fisika. Prinsip dengan aplikasi. Edisi ke -6. Prentice Hall. 106-108.
  2. Resnick, r. (1999). Fisik. Volume 1. Edisi ketiga dalam bahasa Spanyol. Meksiko. Perusahaan Editorial Kontinental S.KE. dari c.V. 67-69.
  3. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Edisi. Meksiko. Editor Pembelajaran Cengage. 84-85.
  4. Geogebra.org