Kecepatan areolar bagaimana itu dihitung dan diselesaikan latihan

Itu Kecepatan areolar Itu adalah area penyapuan per unit waktu dan konstan. Ini adalah tipikal dari masing -masing planet dan muncul dari deskripsi hukum kedua Kepler dengan cara matematika. Dalam artikel ini kita akan menjelaskan apa yang terdiri dari dan bagaimana itu dihitung.

Ledakan yang mewakili penemuan planet di luar tata surya telah mengaktifkan kembali minat pada gerakan planet. Tidak ada yang percaya bahwa planet exo-planet ini mengikuti hukum selain yang sudah diketahui dan valid dari tata surya: hukum Kepler.

Johannes Kepler adalah astronom yang, tanpa bantuan teleskop dan menggunakan pengamatan mentornya Tycho Brahe, menciptakan model matematika yang menggambarkan pergerakan planet -planet di sekitar matahari.

Dia meninggalkan model ini yang diungkapkan dalam tiga undang -undang yang menyandang namanya dan yang tetap valid hari ini seperti pada 1609, ketika dia mendirikan dua dan 1618 yang pertama, tanggal di mana yang ketiga.

[TOC]

Hukum Kepler

Dalam bahasa saat ini, tiga undang -undang Kepler mengatakan seperti ini:

1. Orbit dari semua planet bersifat elips dan matahari menjadi fokus.

2. Vektor posisi yang beralih dari matahari ke planet menyapu area yang sama dalam waktu yang sama.

3. Kuadrat periode orbital sebuah planet sebanding dengan kubus semi-weise elips yang dijelaskan.

Planet akan memiliki kecepatan linier, seperti objek yang diketahui yang bergerak. Dan ada lebih banyak: Saat menulis hukum kedua Kepler dalam bentuk matematika, konsep baru yang disebut areolar speed, tipikal masing -masing planet muncul.

Mengapa planet bergerak secara elips di sekitar matahari?

Bumi dan planet -planet lain bergerak di sekitar matahari berkat fakta bahwa itu memberikan kekuatan pada mereka: daya tarik gravitasi. Hal yang sama berlaku untuk bintang lain dan planet yang sesuai dengan sistem Anda, jika Anda memilikinya.

Itu dapat melayani Anda: panas sensitif: konsep, formula dan latihan diselesaikan

Ini adalah kekuatan dari jenis yang dikenal sebagai gaya pusat. Bobot adalah kekuatan utama yang biasa diketahui semua orang. Objek yang mengerahkan kekuatan pusat, baik itu matahari atau bintang yang jauh, menarik planet ke arah pusat mereka dan mereka bergerak menggambarkan kurva tertutup.

Pada prinsipnya kurva ini dapat diperkirakan sebagai lingkar, seperti Nicolás Copernico, seorang pencipta astronom Polandia dari teori heliosentris,.

Gaya yang bertanggung jawab adalah daya tarik gravitasi. Kekuatan ini tergantung langsung pada massa bintang dan planet yang dimaksud dan berbanding terbalik dengan kuadrat dari jarak yang memisahkan mereka.

Masalahnya tidak begitu mudah, karena dalam tata surya, semua elemen berinteraksi dengan cara ini, menambah kompleksitas pada masalah ini. Mereka juga bukan partikel, karena bintang dan planet berukuran bisa.

Untuk alasan ini, titik sentral orbit atau sirkuit yang dilalui oleh planet-planet tidak persis berpusat pada bintang, tetapi pada titik yang dikenal sebagai pusat gravitasi sistem planet sol.

Orbit yang dihasilkan adalah elips. Gambar berikut menunjukkannya, mengambil sebagai contoh bumi dan matahari:

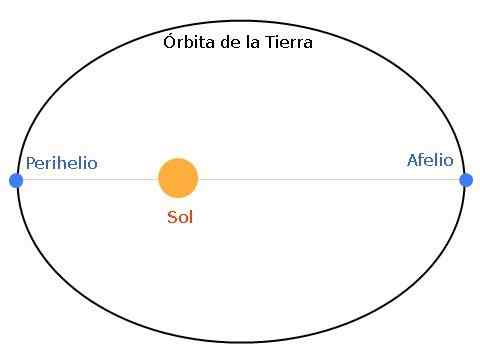Gambar 1. Orbit Bumi adalah elips, dengan matahari yang terletak di salah satu fokus. Ketika Bumi dan Matahari berada pada jarak maksimum dikatakan bahwa Bumi berada di Aphelium. Dan jika jaraknya minimal maka kita berbicara tentang perihelio.

Apelum adalah posisi terjauh dari bumi ke matahari, sedangkan perihelium adalah titik terdekat. Elips bisa lebih atau kurang rata, sesuai dengan karakteristik sistem bintang - planet.

Nilai ASel dan perihelio bervariasi setiap tahun, karena planet lain menyebabkan gangguan. Untuk planet lain, posisi ini masing -masing disebut dukungan dan keahlian.

Besarnya kecepatan linier planet tidak konstan

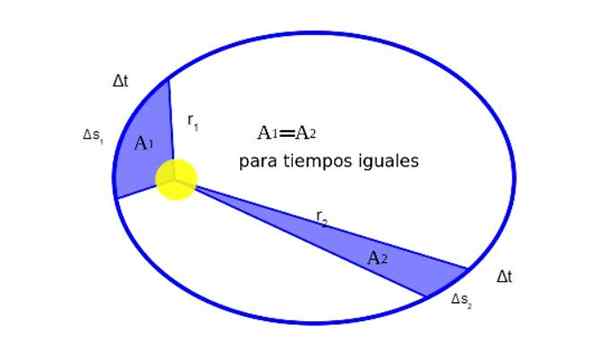
Kepler menemukan bahwa ketika sebuah planet mengorbit di sekitar matahari, selama gerakan barrnya sama dengan area yang sama di waktu yang sama. Gambar 2 secara grafis menunjukkan arti dari ini:

Itu bisa melayani Anda: apa keseimbangan partikel? (Dengan contoh)Gambar 2. Posisi vektor sebuah planet sehubungan dengan matahari adalah r. Saat planet ini menggambarkan orbitnya melakukan busur elips dalam waktu Δt.

Secara matematis, fakta itu₁ menjadi sama dengan₂ Diungkapkan seperti ini:

Rute lengkungan kecil, sehingga setiap area dapat mendekati segitiga:

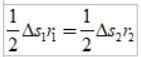
Sebagai ΔS =vΔT, Di mana v adalah kecepatan linier planet pada titik tertentu, saat mengganti kita memiliki:

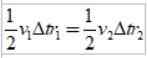
Dan karena interval waktu ΔT adalah sama, diperoleh:

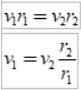
Seperti r₂ > r₁, lalu v₁ > v₂, Dengan kata lain, kecepatan linier sebuah planet tidak konstan. Faktanya, Bumi berjalan lebih cepat saat berada di perihelium daripada saat berada di aphelium.

Oleh karena itu kecepatan linier bumi atau planet mana pun di sekitar matahari bukanlah besarnya yang berfungsi untuk mengkarakterisasi pergerakan planet tersebut.

Kecepatan areolar

Hukum kedua Kepler menunjukkan besarnya baru yang disebut kecepatan areolar. Itu didefinisikan sebagai area yang disapu per unit waktu dan konstan. Untuk menghitungnya, gambar berikut digunakan:

Gambar 3. Vektor posisi bumi (atau planet) sehubungan dengan matahari adalah r, dan saat bergerak, bumi mengalami perpindahan, juga vektor Δr.

Area kecil yang disapu bumi dipilih saat melakukan sirkuit elipsnya, yang akan kami tunjukkan bagaimana Δa. Waktu yang dibutuhkan untuk ini adalah Δt.

Gambar 3 menunjukkan vektor posisi bumi sehubungan dengan matahari, dilambangkan dengan r. Saat bumi bergerak, alami perpindahan ΔR.

Area ini sesuai dengan setengah dari area persegi panjang yang ditunjukkan pada Gambar 3:

Hasil bagi Δr/Δt justru kecepatan linier bumi, sehingga kecepatan areolar tetap:

V_KE Dalam sistem internasional mereka:

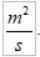
Perhatikan bahwa sementara baik R dan V bervariasi, produk tetap konstan. Ini mengubah kecepatan areolar menjadi besarnya yang sangat cocok untuk mengkarakterisasi pergerakan planet di sekitar bintangnya.

Dapat melayani Anda: Konstanta Antoine: Rumus, Persamaan, Contoh

Produk R dan V adalah besarnya momentum sudut L, sehingga kecepatan areolar dapat dinyatakan sebagai:

Menghitung kecepatan linier dan kecepatan areolar

Dengan contoh berikut, kami akan menunjukkan cara menghitung kecepatan areolar ketika beberapa parameter gerakan planet diketahui:

Latihan

Exo-planet bergerak di sekitar matahari setelah orbit elips, menurut hukum Kepler. Saat berada di Expertro, vektor radionya adalah R₁ = 4 · 10⁷ km, dan saat mendukungnya adalah r₂ = 15 · 10⁷ km. Kecepatan linier dalam keahliannya adalah v₁ = 1000 km/s.

Menghitung:

A) besarnya kecepatan dalam dukungan.

B) kecepatan areolar dari planet exo.

C) Panjang elips mayor semi -axis.

Jawaban untuk)

Persamaan digunakan:

di mana nilai numerik diganti.

Setiap istilah diidentifikasi sebagai berikut:

v₁ = Kecepatan dalam dukungan; v₂ = Kecepatan di ahli; r₁= Jarak Penulis,

R₂= Jarak dari ahli.

Dengan nilai -nilai ini diperoleh:

Jawab B)

Persamaan yang akan digunakan adalah

di mana pasangan nilai r dan v dari ekspertro atau dukungan dapat diganti, karena v_KE Itu adalah konstanta planet:

Jawaban C)

Panjang semi -axle utama elips adalah semi -semi -semi -semi -semi -seismum dan keahlian:

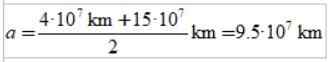
Bibliografi

1. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. Meksiko. Editor Pembelajaran Cengage. 367-372.
2. Stern, d. (2005). Tiga hukum Kepler dari gerakan planet. Diperoleh dari PWG.GSFC.pot.Pemerintah
3. Catatan: Latihan yang diusulkan diambil dan dimodifikasi dari teks buku McGrawhill berikut. Sayangnya ini adalah bab yang terisolasi dalam format PDF, tanpa judul atau penulis: Mheducation.ES/BCV/Panduan/Bab/844817027x.Pdf