Apa bagian dari pesawat Cartesian?

Itu bagian dari pesawat Cartesian Mereka terdiri dari dua garis nyata dan tegak lurus, yang membagi bidang Cartesian menjadi empat wilayah. Masing -masing daerah ini disebut kuadran dan unsur -unsur bidang Cartesian disebut titik. Pesawat, bersama dengan sumbu koordinat, dipanggil Pesawat Cartesian Untuk menghormati filsuf Prancis René Descartes, yang menemukan geometri analitik.

Dua garis (atau sumbu koordinat) tegak lurus karena mereka membentuk sudut 90º di antara mereka dan menyeberang ke titik yang sama (asal). Salah satu garis adalah horizontal, disebut asal X (atau abcisa) dan garis lainnya vertikal, disebut asal y (atau dipesan).

Setengah positif dari sumbu x adalah di sebelah kanan asal dan setengah positif dari sumbu y adalah asal. Ini memungkinkan membedakan empat kuadran bidang Cartesian yang sangat berguna saat titik grafik di pesawat.

Titik pesawat Cartesian

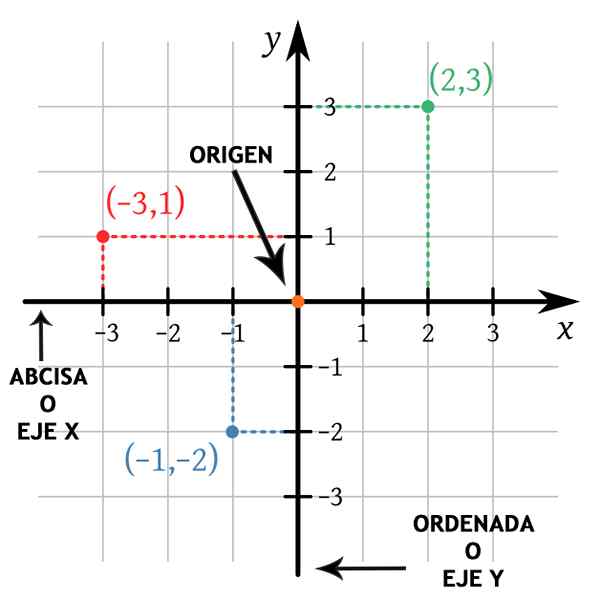
Di setiap titik P Pesawat dapat diberikan beberapa bilangan real yang merupakan koordinat cartesiannya.

Jika garis horizontal dan garis vertikal melewati P, Dan Anda berpotongan di X dan sumbu ke sumbu y ke Dan B masing -masing, kemudian koordinat P adalah (ke,B). Itu dipanggil ke (ke,B) Pasangan tertib dan urutan di mana angka -angka itu ditulis penting.

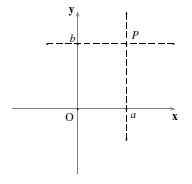
Nomor pertama, ke, Ini adalah koordinat dalam "x" (atau absis) dan angka kedua, B, Itu adalah koordinat dalam "y" (atau dipesan). Notasi digunakan P = (ke,B).

Terbukti dengan cara di mana bidang Cartesian dibangun bahwa asal -usulnya sesuai dengan sumbu "x" dan 0 dalam sumbu "y", yaitu, yaitu,, SALAH SATU= (0,0).

Cuadies dari pesawat Cartesian

Seperti dapat dilihat pada angka -angka sebelumnya, sumbu koordinat menghasilkan empat daerah berbeda yang merupakan kuadran bidang Cartesian, yang dilambangkan dengan huruf dan, Ii, iii Dan Iv Dan ini berbeda satu sama lain dalam tanda yang dimiliki poin -poin yang ada di masing -masing.

Kuadran yo

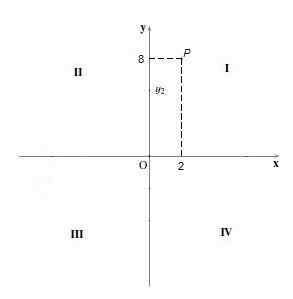
Titik -titik kuadran yo Mereka adalah mereka yang memiliki kedua koordinat dengan tanda positif, yaitu koordinat x mereka dan koordinat mereka dan positif.

Misalnya, intinya P = (2.8). Untuk membuat grafik, titik 2 terletak pada sumbu "x" dan titik 8 pada sumbu "y", kemudian garis vertikal dan horizontal ditarik masing -masing, dan di mana mereka berpotongan adalah tempat titik berada berada P.

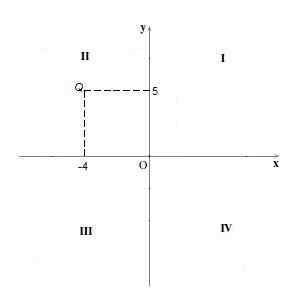
Kuadran Ii

Titik -titik kuadran Ii Mereka memiliki koordinat "x" negatif dan koordinat "y" positif. Misalnya, intinya Q = (-4.5). Ini adalah proses grafis seperti pada kasus sebelumnya.

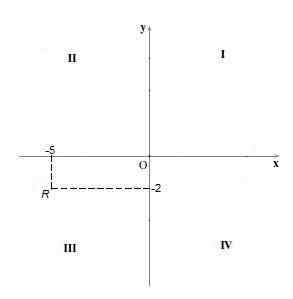
Kuadran AKU AKU AKU

Di kuadran ini tanda kedua koordinat adalah negatif, yaitu, koordinat "x" dan koordinat "y" yang dimiliki negatif. Misalnya, titik r = (-5, -2).

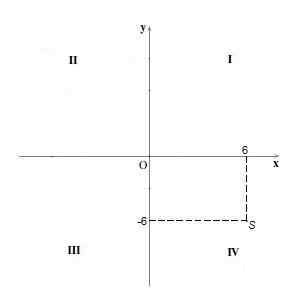
Kuadran Iv

Di kuadran Iv Poin memiliki koordinat negatif "y" yang positif dan koordinat. Misalnya intinya S = (6, -6).

Referensi

1. Fleming, w., & Varberg, D. (1991). Aljabar dan trigonometri dengan geometri analitik. Pendidikan Pearson.
2. Larson, r. (2010). Prealculus (8 ed.). Pembelajaran Cengage.
3. Loyal, J. M., & Viloria, n. G. (2005). Geometri analitik datar. Mérida - Venezuela: Editorial Venezuela C. KE.
4. Oteyza, e. (2005). Geometri analitik (Ed kedua.). (G. T. Mendoza, ed.) Pendidikan Pearson.
5. Oteyza, e. D., Osnaya, e. L., Garciadiego, c. H., Hoyo, a. M., & Flores, untuk. R. (2001). Geometri analitik dan trigonometri (Ed pertama.). Pendidikan Pearson.
6. Purcell, e. J., VARBERG, D., & Rigdon, s. DAN. (2007). Perhitungan (Edisi kesembilan.). Prentice Hall.
7. Scott, c. KE. (2009). Geometri Pesawat Cartesian, Bagian: Analytical Conics (1907) (Cetak ulang ed.). Sumber petir.