Persamaan Kuadrat Rumus Umum, Contoh, Latihan

Itu Formula Umum, yang juga dikenal sebagai Formula pelarut Dalam beberapa teks, ini digunakan untuk menyelesaikan persamaan tingkat kedua: kapak² + bx + c = 0.

Di dalamnya ke, B Dan C Mereka adalah bilangan real, dengan kondisi itu ke berbeda dari 0, menjadi X Yang tidak diketahui. Kemudian, rumus umum menyajikan pembersihan yang tidak diketahui melalui ekspresi yang melibatkan nilai -nilai ke, B Dan C sebagai berikut:

Gambar 1. Rumus umum dalam matematika digunakan untuk menyelesaikan persamaan kuadrat. Sumber: f. Zapata.

Dan melalui formula ini Anda dapat menemukan solusi dari setiap persamaan tingkat kedua atau kuadratik, asalkan solusi tersebut ada.

Menurut sejarawan, formula umum sudah dikenal oleh matematika Babel kuno. Itu kemudian ditransmisikan ke orang lain, seperti orang Mesir dan orang -orang Yunani, melalui pertukaran budaya.

Formula dan variannya tiba di Eropa berkat ahli matematika Muslim yang menetap di Semenanjung Iberia. Namun, mereka tidak menggunakan notasi aljabar yang saat ini kami gunakan. Notasi ini disebabkan oleh ahli matematika Prancis dan ahli kriptografi abad ke -16 Francois Viete.

[TOC]

Persamaan kuadrat dengan formula umum

Mari kita lihat bagaimana formula umum muncul, untuk memverifikasi validitasnya. Mulai dari persamaan kuadratik umum:

kapak² + bx + c = 0

Mari kita praktikkan beberapa manipulasi aljabar sederhana, untuk mencapai pembersihan yang tidak diketahui. Ada beberapa cara untuk membawa ini, misalnya menyelesaikan kotak, seperti yang ditunjukkan saat itu.

Demonstrasi formula umum

Kita mulai dengan menambahkan (-c) di kedua sisi kesetaraan:

kapak² + Bx = - c

Dan sekarang dikalikan dengan 4a, selalu di kedua sisi kesetaraan, agar tidak mengubah ekspresi:

4² X² + 4ab x = - 4ac

Menambahkan b²:

4²⋅x² + 4ab⋅x + b² = - 4ac + b²

Tujuan dari ini adalah untuk menyelesaikan kotak di sisi kiri kesetaraan, yang berisi yang tidak diketahui, dengan cara ini izinnya difasilitasi. Dengan demikian:

Dapat melayani Anda: pembagi 8: apa itu dan penjelasan yang mudah

-Istilah pertama: ke -4² X² Itu adalah kuadrat sempurna 2AX

-Yang terakhir, yaitu b², Itu adalah kuadrat yang sempurna dari b.

-Dan istilah pusat adalah produk ganda dari 2ax dan b: 2⋅2ax⋅b = 4abx

Karena itu kami memiliki binomial persegi:

4²⋅x² + 4ab⋅x + b² = (2ax + b)²

Dan kita bisa menulis:

(2ax + b)² = - 4ac + b²

Kami satu langkah dari membersihkan yang tidak diketahui X:

Dan kami sudah mendapatkan formula umum yang kami tahu:

Ada cara lain untuk memanipulasi persamaan kuadratik secara aljabar dan mendapatkan hasil yang sama ini.

Contoh Penggunaan Formula Umum

Untuk menerapkan rumus umum, nilai A, B dan C ditentukan dengan cermat dan diganti dalam formula. Perhatikan simbolnya kurang lebih di pembilang; Ini menunjukkan bahwa kita harus mempertimbangkan dua kemungkinan mengenai operasi, satu dengan tanda + dan satu dengan tanda -.

Persamaan kuadratik dapat memiliki solusi berikut, sesuai dengan nilai kuantitas sub-radikal, yang dikenal sebagai membedakan:

-Ya b² - 4ac> 0, persamaan kuadratik memiliki dua solusi nyata dan berbeda.

-Ketika b² - 4ac = 0, persamaan memiliki solusi unik, diberikan oleh:

x = -b/2a

-Akhirnya, jika b² - 4ac < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Mari kita lihat beberapa contoh di mana formula umum diterapkan, memperhatikan bahwa jika ada koefisien yang menyertai yang tidak diketahui tidak muncul, dipahami bahwa itu bernilai 1. Dan jika istilah independen adalah yang tidak ditemukan, maka itu bernilai 0.

- Contoh 1

Selesaikan persamaan kuadratik berikut:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Menjawab

Kami menulis koefisien setiap istilah: A = 6, b = 11, c = -10 dan mengganti nilai dalam rumus umum:

Dapat melayani Anda: pajak

x = (-11 ± 19) /12

Hasilnya mengarah ke dua solusi nyata berikut:

X₁ = (-11 + 19)/12 = 8/12 = 2/3

X₂ = (-11 -19)/12 = -5/2

Jawaban b

Sekali lagi koefisien ditentukan: a = 3, b = -5 dan c = -1. Dengan mengganti dalam formula:

Berbeda dengan kasus sebelumnya, akar kuadrat dari 37 bukan bilangan bulat, tetapi kami juga dapat meningkatkan kedua solusi dan meninggalkan akar atau menemukan nilai desimal yang sesuai dengan bantuan kalkulator:

X₁ = (-5 + √37)/6 ≈ 0.18

X₂ = (-5 - √37)/6 ≈ - 1.85

- Contoh 2

Selesaikan persamaan tingkat kedua x² - 4x +13 = 0.

Menjawab

Seperti biasa, kami mengidentifikasi nilai -nilai koefisien dan mengganti rumus umum: A = 1, b = - 4, c = 13. Ini mengarah ke:

Kami memiliki akar negatif, oleh karena itu solusi dari persamaan ini adalah bilangan yang kompleks. Akar dapat dinyatakan dalam hal yo, itu Unit imajiner:

√ (36i²) = 6i

Sejak aku² = -1, oleh karena itu solusi kompleksnya adalah:

X₁ = (4 + 6i)/2 = 2 + 3i

X₂ = (4 - 6i)/2 = 2 - 3i

Olahraga diselesaikan

Tangga panjang 10 m bersandar pada dinding vertikal, dengan kaki 6 m dari dinding itu. Tangga slip dan kaki dipisahkan 3 m lebih dari pangkalan.

Temukan jarak vertikal yang berjalan melalui bagian atas tangga.

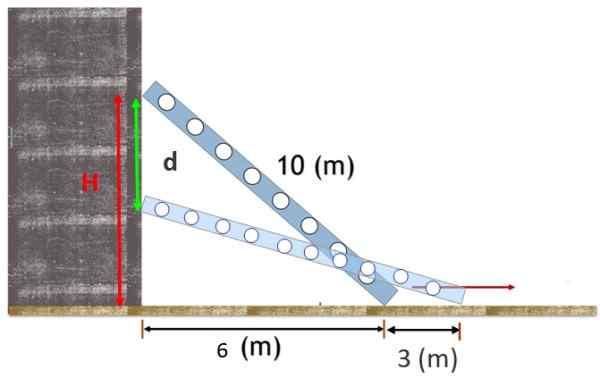Gambar 2. Tangga yang didukung di dinding sedikit tergelincir dan pemberhentian atas bergerak secara vertikal ke bawah jarak D. Sumber: f. Zapata.

Larutan

Untuk menemukan jarak vertikal yang menggeser bagian atas tangga, Anda harus menemukan posisi di mana itu awalnya mengenai tanah. Kita bisa melakukannya dengan teorema Pythagoras, karena sosok yang terbentuk adalah dari segitiga kanan:

H = (10² - 6²) ^½ = 8 m

Setelah tangga tergelincir, jarak bergerak D, Ukur karena bagian atas setinggi 8 m, sampai mencapai posisi barunya, pada (H-D) meter di atas tanah. Yang tidak diketahui membersihkan adalah D.

Dapat melayani Anda: frekuensi akumulasi: rumus, perhitungan, distribusi, contoh

Untuk menemukannya, kami mengusulkan segitiga persegi panjang baru, yang terbentuk setelah tangga tergelincir sedikit. Segitiga ini masih memiliki hipotenusa sama dengan 10 m dan kateto paralel sekarang 6m + 3m = 9 m, oleh karena itu: oleh karena itu:

(H-D)² = 10² - 9² = 100 - 81 = 19

Kami mengganti h = 8m, yang sebelumnya dihitung:

(8-D)² = 19

Persamaan dapat diselesaikan dalam beberapa cara, termasuk penggunaan formula umum, yang akan kami tunjukkan di bawah ini dengan langkah -langkah ini:

Langkah 1

Kembangkan kiri terkenal dari kiri:

64 -16D + D² = 19

Langkah 2

Menetapkan persamaan tingkat kedua untuk d:

D² - 16d + 45 = 0

Langkah 3

-Koefisiennya adalah: a = 1, b = -16 dan c = 45, kami menggantinya dalam rumus umum:

Solusi persamaannya adalah:

D₁ = (16 + √76)/2 ≈ 12.36 m

D₂ = (16 - √76)/2 ≈ 3.64 m

Langkah 4

Solusi yang diperoleh dianalisis: yang pertama tidak masuk akal secara fisik, karena tidak mungkin bagi tangga untuk mengkompilasi 12.36 m, jika awalnya berhenti setinggi 8 m di tanah.

Oleh karena itu, jawaban yang benar adalah solusi kedua: bagian atas tangga slip d = 3.64 m.

Dapatkah pembaca memecahkan masalah dengan menerapkan metode lain?

Referensi

1. Baldor. 1977. Aljabar Dasar. Edisi Budaya Venezuela.
2. Hoffman, J. Pemilihan masalah matematika. Volume 2.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.