Properti Fungsi Logaritmik, Contoh, Latihan

Itu fungsi logaritmik Ini adalah hubungan matematika yang mengaitkan setiap bilangan real positif X Dengan logaritma Anda Dan di pangkalan ke. Hubungan ini memenuhi persyaratan untuk menjadi suatu fungsi: setiap elemen x milik domain memiliki gambar yang unik.

Karena itu:

f (x) = y = log_ke X , Dengan> 0 dan berbeda dari 1.

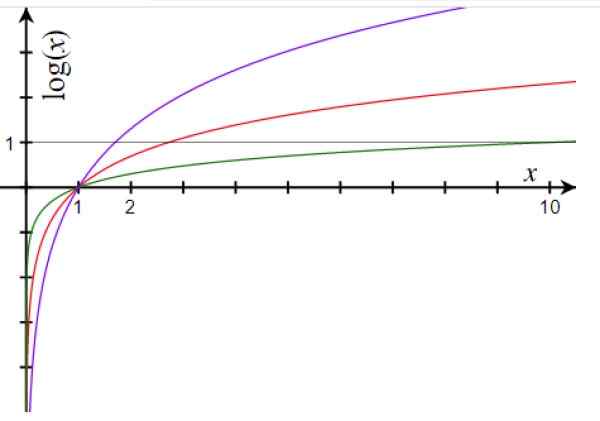
Gambar 1. Grafik Fungsi Logaritma untuk Basis 10 (Hijau), Basis E (Merah) dan Basis 1.7 (ungu). Sumber: Wikimedia Commons.

Sifat utama fungsi logaritmik adalah:

-Domainnya adalah semua yang lebih besar dari 0, tidak termasuk 0. Dengan kata lain, tidak ada logaritma atau angka negatif di pangkalan apa pun. Dalam bentuk interval:

Matahari _F = (0, ∞+)

-Logaritma angka bisa negatif, positif atau 0, sehingga jangkauan atau rutanya adalah:

Rgo _F = (-∞, ∞+)

-Fungsi logaritmik selalu tumbuh untuk> 1 dan menurun<1.

-Kebalikan dari f (x) = log_ke X adalah fungsi eksponensial.

Memang, fungsi logaritma berdasarkan, adalah fungsi terbalik dari fungsi potensial:

F^-1(x) = a^Dan

Sejak berbasis logaritma ke dari angka X, Itu angkanya Dan yang harus diangkat pangkalan ke mendapatkan X.

-Logaritma dasar selalu 1. Dengan demikian, grafik f (x) = log_ke X Selalu berpotongan ke sumbu x pada titik (1.0)

-Fungsi logaritmik adalah transenden dan tidak dapat dinyatakan sebagai polinomial atau sebagai hasil bagi ini. Selain logaritma, grup ini mencakup fungsi trigonometri dan eksponensial, antara lain.

[TOC]

Contoh

Fungsi logaritmik dapat ditetapkan melalui berbagai basis, tetapi yang paling banyak digunakan adalah 10 dan Dan, Di mana Dan Itu adalah jumlah euler yang sama dengan 2.71828 .. .

Saat pangkalan 10 digunakan, logaritma disebut logaritma desimal, logaritma vulgar, briggs atau sekadar logaritma untuk mengeringkan.

Dan jika angka E digunakan, maka itu disebut Neperian Logaritma, oleh John Napier, ahli matematika Skotlandia yang menemukan logaritma.

Dapat melayani Anda: invers multiplikasi: penjelasan, contoh, latihan terpecahkan

Notasi yang digunakan untuk masing -masing adalah sebagai berikut:

-Logaritma desimal: log₁₀ x = log x

-Logaritma Neperian: ln x

Ketika basis lain akan digunakan, itu benar -benar diperlukan. Misalnya, jika itu tentang logaritma di base 2, itu ditulis:

y = log₂ X

Mari kita lihat logaritma nomor 10 dalam tiga pangkalan yang berbeda, untuk mengilustrasikan poin ini:

Log 10 = 1

Ln 10 = 2.30259

catatan₂ 10 = 3.32193

Kalkulator umum hanya membawa logaritma desimal (log) dan logaritma Neperian (fungsi LN). Di internet ada kalkulator dengan basis lain. Bagaimanapun, pembaca dapat memverifikasi, dengan bantuan yang sama, bahwa dengan nilai -nilai sebelumnya dipenuhi:

10¹ = 10

Dan^2.3026 = 10.0001

2^3.32193 = 10.0000

Perbedaan desimal kecil disebabkan oleh jumlah desimal yang diambil dalam perhitungan logaritma.

Keuntungan logaritma

Di antara keuntungan menggunakan logaritma adalah kemudahan yang mereka berikan untuk bekerja dengan jumlah besar, menggunakan logaritma mereka alih -alih nomornya secara langsung.

Ini dimungkinkan karena fungsi logaritma tumbuh lebih lambat karena angkanya lebih besar, seperti yang kami hargai dalam grafik.

Jadi bahkan dalam kasus jumlah yang sangat besar, logaritma mereka jauh lebih kecil, dan memanipulasi jumlah kecil selalu lebih mudah.

Selain itu, logaritma memenuhi properti berikut:

-Produk: log (a.b) = log a + log b

-Hasil bagi: log (a/b) = log a - log b

-Kekuatan: log a^B = b.log a

Dan dengan cara ini, produk dan quotient menjadi jumlah dan pengurangan angka yang lebih kecil, sementara potensiasi diubah menjadi produk sederhana meskipun daya tinggi.

Itulah sebabnya logaritma memungkinkan untuk mengekspresikan angka yang bervariasi dalam rentang nilai yang sangat besar, seperti intensitas suara, pH larutan, kecerahan bintang, ketahanan listrik dan intensitas gempa bumi pada Richter skala.

Dapat melayani Anda: sudut alternatif eksternal: latihan dan latihan diselesaikanGambar 2. Logaritma digunakan pada skala Richter untuk mengukur besarnya gempa bumi. Gambar tersebut menunjukkan sebuah bangunan runtuh di Concepción, Chili, selama gempa bumi 2010. Sumber: Wikimedia Commons.

Mari kita lihat contoh penanganan properti logaritma:

Contoh

Temukan nilai x dalam ekspresi berikut:

Log (5x +1) = 1 + log (2x-1)

Menjawab

Kami memiliki persamaan logaritmik di sini, mengingat fakta bahwa yang tidak diketahui ada di argumen logaritma. Itu diselesaikan dengan meninggalkan satu logaritma di setiap sisi kesetaraan.

Kita mulai dengan menempatkan semua istilah yang berisi "x" di sebelah kiri kesetaraan, dan yang hanya berisi angka di sebelah kanan:

Log (5x+1) - Log (2x -1) = 1

Di sebelah kiri kita memiliki pengurangan dua logaritma, yang dapat ditulis sebagai logaritma hasil bagi:

log [(5x+1)/ (2x-1)] = 1

Namun, di sebelah kanan adalah nomor 1, yang dapat kita ungkapkan sebagai log 10, seperti yang kita lihat sebelumnya. Jadi:

log [(5x+1)/ (2x-1)] = log 10

Agar kesetaraan dipenuhi, argumen logaritma harus sama:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Latihan Aplikasi: Skala Richter

Pada tahun 1957 gempa bumi terjadi di Meksiko yang besarnya 7.7 dalam skala Richter. Pada tahun 1960 gempa bumi paling besar lainnya terjadi di Chili, 9.5.

Hitung berapa kali gempa bumi Chili lebih intens daripada Meksiko, mengetahui bahwa besarnya m_R Pada skala Richter diberikan oleh formula:

M_R = log (10⁴ YO)

Larutan

Besarnya dalam skala gempa richter adalah fungsi logaritmik. Kami akan menghitung intensitas setiap gempa bumi, karena kami memiliki magnitudo Richter. Mari kita lakukan langkah demi langkah:

Dapat melayani Anda: bilangan primo: karakteristik, contoh, latihan

-Meksiko: 7.7 = log (10⁴ YO)

Karena kebalikan dari fungsi logaritma adalah eksponensial, kami menerapkan ini di kedua sisi kesetaraan dengan maksud membersihkan i, yang ditemukan dalam argumen logaritma.

Karena mereka adalah logaritma desimal, dasarnya 10. Jadi:

Dalam istilah kanan, 10 dan log (10⁴ I) Mereka dibatalkan (seperti halnya akar kuadrat dan persegi), menjadi: meninggalkan:

10 ^7.7 = 10⁴ yo

Intensitas gempa bumi Meksiko adalah:

yo_M = 10 ^7.7 / 10⁴ = 10^3.7

 -Cabai: 9.5 = log (10⁴ YO)

Prosedur yang sama membawa kita ke intensitas gempa bumi Chili i_Ch:

yo_Ch = 10 ^9.5 / 10⁴ = 10^5.5

 Sekarang kita dapat membandingkan kedua intensitas:

yo_Ch / YO_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 yo_Ch = 63.1. yo_M

Gempa Bumi Chili sekitar 63 kali lebih intens daripada Meksiko. Karena besarnya logaritmik, ia tumbuh lebih lambat dari intensitas, maka perbedaan 1 dalam besarnya berarti amplitudo 10 kali lebih besar dari gelombang seismik.

Perbedaan antara besaran kedua gempa adalah 1.8, oleh karena itu kita bisa mengharapkan perbedaan intensitas yang lebih dekat ke 100 dari hingga 10, seperti yang secara efektif terjadi.

Faktanya, jika perbedaannya tepat 2, gempa bumi Chili akan 100 kali lebih intens daripada orang Meksiko.

Referensi

1. Carena, m. 2019. Manual Matematika Preuniversity. Universitas Nasional Pantai.
2. Figuera, J. 2000. Matematika 1. Tahun yang beragam. Edisi Co-Bo.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
5. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.