Homosedisitas apa, penting dan contoh

Itu Homosedisitas Dalam model statistik prediktif itu terjadi jika dalam semua kelompok data dari satu atau lebih pengamatan, varian model sehubungan dengan variabel penjelas (atau independen) tetap konstan.

Model regresi bisa homokedastik atau tidak, dalam hal ini kita bicarakan heterosedisitas.

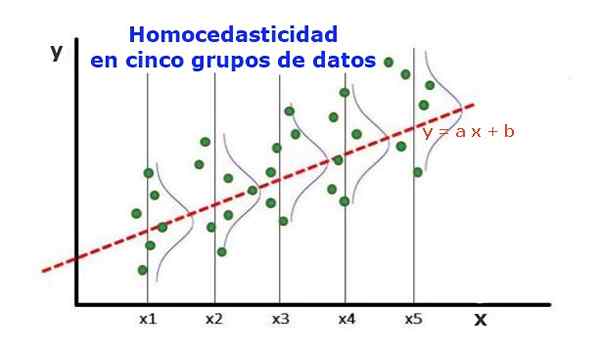
Gambar 1. Lima grup data dan penyesuaian regresi dari set. Varians mengenai nilai yang diprediksi adalah sama di setiap kelompok. (UPAV-LIBER.org)

Model regresi statistik dari beberapa variabel independen disebut homokedastik, hanya jika varians dari kesalahan variabel yang diprediksi (atau standar deviasi variabel dependen) tetap seragam untuk kelompok yang berbeda dari variabel penjelas atau independen.

Dalam lima kelompok data pada Gambar 1, varians telah dihitung dalam setiap kelompok, sehubungan dengan nilai yang diperkirakan oleh regresi, berubah menjadi sama di setiap kelompok. Juga diasumsikan bahwa data mengikuti distribusi normal.

Pada tingkat grafik itu berarti bahwa titik -titik tersebut sama -sama tersebar atau tersebar di sekitar nilai yang diprediksi dengan penyesuaian regresi, dan bahwa model regresi memiliki kesalahan dan validitas yang sama untuk kisaran variabel penjelas.

[TOC]

Pentingnya homosedisitas

Untuk menggambarkan pentingnya homosedastisitas dalam statistik prediktif, perlu untuk kontras dengan fenomena yang berlawanan, heterokedisitas.

Homosedastik versus heterosedisitas

Dalam kasus Gambar 1, di mana ada homoseditas, dipenuhi bahwa:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Di mana var ((yi-ii); xi) mewakili varian, pasangan (xi, yi) mewakili fakta grup I, sedangkan yi adalah nilai yang memprediksi regresi untuk nilai xi rata-rata grup. Varian data grup I dihitung sebagai berikut:

Var ((yi -ii); xi) = ∑J (yij - yi)^2/n

Sebaliknya, ketika heterosedisitas terjadi, model regresi mungkin tidak berlaku untuk seluruh wilayah di mana ia dihitung. Gambar 2 menunjukkan contoh situasi ini.

Dapat melayani Anda: apa itu sudut alternatif internal? (Dengan latihan)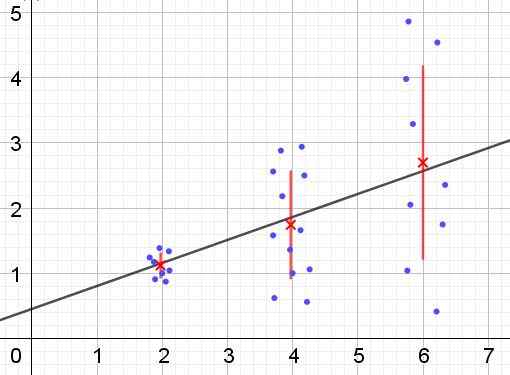 Gambar 2. Grup data yang memiliki heterosedisitas. (Elaborasi sendiri)

Pada Gambar 2 tiga kelompok data dan himpunan set diwakili oleh regresi linier. Perlu dicatat bahwa data di kelompok kedua dan dalam kelompok ketiga lebih tersebar daripada di kelompok pertama. Grafik Gambar 2 juga menunjukkan nilai rata -rata masing -masing kelompok dan bilah kesalahannya ± σ, menjadi standar deviasi σ dari setiap grup data. Harus diingat bahwa standar deviasi σ adalah akar kuadrat dari varian.

Jelas bahwa dalam kasus heterosedisitas, kesalahan estimasi regresi berubah dalam kisaran nilai variabel penjelas atau independen, dan dalam interval di mana kesalahan ini sangat besar, prediksi dengan regresi tidak dapat diandalkan atau tak dapat diterapkan.

Dalam model regresi, kesalahan atau limbah (y -y) harus didistribusikan dengan varians yang sama (σ^2) di seluruh interval nilai variabel independen. Karena alasan inilah model regresi yang baik (linear atau non -linear) harus lulus uji homosedastisitas. 

Tes homosedisitas

Poin yang ditunjukkan pada Gambar 3 sesuai dengan data penelitian yang mencari hubungan antara harga (dalam dolar) rumah tergantung pada ukuran atau area dalam meter persegi.

Model pertama yang dilatih adalah regresi linier. Pertama -tama dicatat bahwa koefisien penentuan r^2 dari penyesuaian cukup tinggi (91%), sehingga dapat dianggap bahwa penyesuaian memuaskan.

Namun, dua daerah dapat dibedakan dengan jelas dari grafik penyesuaian. Salah satunya, yang di sebelah kanan terkunci dalam oval, bertemu homosedastisitas, sedangkan wilayah kiri tidak memiliki homosedastisitas.

Dapat melayani Anda: tingkat polinomial: bagaimana itu ditentukan, contoh dan latihan

Ini berarti bahwa prediksi model regresi memadai dan dapat diandalkan dalam kisaran antara 1800 m^2 hingga 4800 m^2 tetapi sangat tidak memadai di luar wilayah ini. Di area heterokedi tidak hanya kesalahannya sangat besar, tetapi juga data tampaknya mengikuti tren lain yang berbeda dari yang diusulkan oleh model regresi linier.

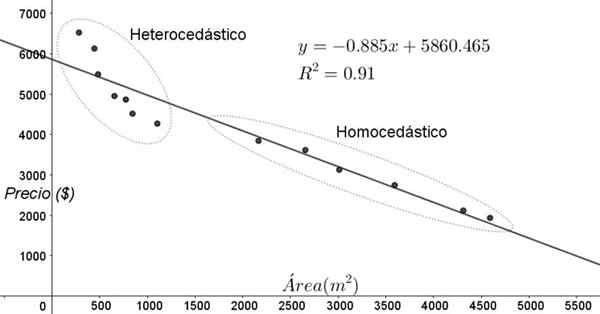Gambar 3. Harga Perumahan vs Area dan Model Prediktif dengan Regresi Linier, menunjukkan area homosedastisitas dan heterosedisitas. (Elaborasi sendiri)

Grafik dispersi data adalah uji homokedastik yang paling sederhana dan paling sederhana, namun kadang -kadang tidak terbukti seperti dalam contoh yang ditunjukkan pada Gambar 3, perlu untuk menggunakan grafik dengan variabel tambahan.

Variabel standar

Dengan tujuan memisahkan area di mana homosedastisitas dipenuhi dan di mana tidak, variabel standar Zres dan zreded diperkenalkan:

Zres = abs (y - y)/σ

Zpred = y/σ

Perlu dicatat bahwa variabel -variabel ini tergantung pada model regresi yang diterapkan, karena itu adalah nilai prediksi regresi. Di bawah ini adalah grafik dispersi Zres vs Zred untuk contoh yang sama:

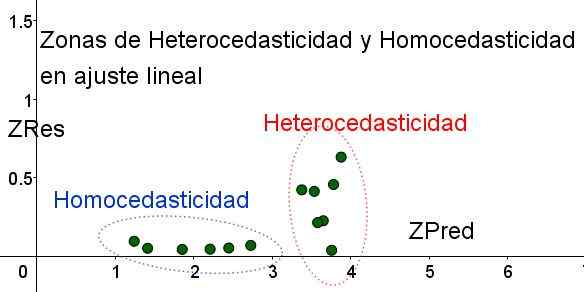Gambar 4. Perlu dicatat bahwa di zona homosedastisitas Zres tetap seragam dan kecil di wilayah prediksi (elaborasi sendiri).

Dalam grafik Gambar 4 dengan variabel standar, area di mana kesalahan residu kecil dan seragam dipisahkan dengan jelas, sehubungan dengan yang tidak. Di area pertama, homosedastisitas dipenuhi sementara kesalahan residu sangat bervariasi dan besar.

Penyesuaian regresi diterapkan pada grup data yang sama 3. Hasilnya ditunjukkan pada gambar berikut:

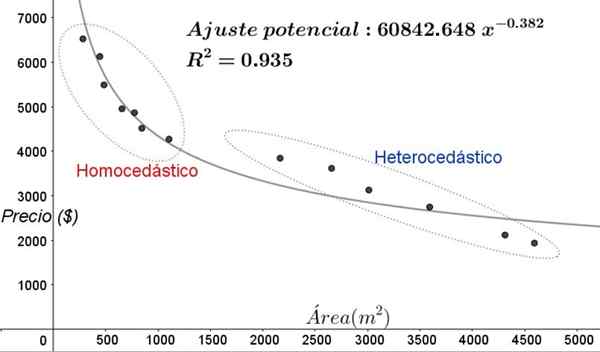Gambar 5. Area homosedastisitas dan heterosedisitas baru dalam penyesuaian data dengan model regresi non-lineal. (Elaborasi sendiri).

Dalam grafik Gambar 5, daerah homosedi dan heterocedicastic harus diperhatikan dengan jelas. Perlu juga dicatat bahwa area ini dipertukarkan sehubungan dengan yang dibentuk dalam model penyesuaian linier.

Dapat melayani Anda: jenis sudut, karakteristik, dan contoh

Dalam grafik Gambar 5 jelas bahwa bahkan ketika ada koefisien penentuan penyesuaian cukup tinggi (93,5%), model ini tidak cocok untuk seluruh interval variabel penjelas, karena data untuk nilai yang lebih tua dari 2000 m^2 memiliki heterokedastisitas.

Tes homokedastisitas non -pepa

Salah satu tes nonografi yang paling banyak digunakan untuk memverifikasi apakah homosedastisitas terpenuhi adalah atau tidak adalah Tes Breusch-Pagan.

Semua detail tes ini tidak akan diberikan dalam artikel ini tetapi karakteristik fundamentalnya dan langkah -langkah yang sama diuraikan secara luas:

1. Model regresi diterapkan pada data N dan varian yang sama dihitung sehubungan dengan nilai yang diperkirakan oleh model σ^2 = ∑J (yj - y)^2/n.
2. Variabel baru ε = ((yj - y)^2) / (σ^2) didefinisikan
3. Model regresi yang sama diterapkan pada variabel baru dan parameter regresi baru dihitung.
4. Nilai kritis chi kuadrat (χ^2) ditentukan, ini menjadi setengah dari jumlah limbah baru dalam variabel ε.
5. Tabel distribusi chi square digunakan dengan mempertimbangkan tingkat signifikansi pada sumbu x (biasanya 5%) dan jumlah derajat kebebasan (variabel regresi #of kecuali unit), untuk mendapatkan nilai papan.
6. Nilai kritis yang diperoleh pada Langkah 3 dibandingkan dengan nilai yang ditemukan dalam tabel (χ^2).
7. Jika nilai kritis di bawah tabel Anda memiliki hipotesis nol: ada homosedisitas
8. Jika nilai kritis di atas tabel Anda memiliki hipotesis alternatif: tidak ada homosedastisitas.

Sebagian besar paket komputer statistik seperti: SPSS, Minitab, R, Python Pandas, SAS, StatGraphic dan beberapa lainnya menggabungkan uji homosedastisitas Breusch-Pagan. Tes lain untuk memverifikasi keseragaman varian Tes Levene.

Referensi

1. Kotak, Pemburu & Pemburu. (1988) Statistik untuk peneliti. Saya membalikkan editor.
2. Johnston, J (1989). Metode Ekonometrika, Vicens -Ives Editor.
3. Murillo dan González (2000). Manual Ekonometri. Universitas Las Palmas de Gran Canaria. Diperoleh dari: ULPGC.adalah.
4. Wikipedia. Homosedisitas. Pulih dari: is.Wikipedia.com
5. Wikipedia. Homoskedastisitas. Diperoleh dari: di.Wikipedia.com