Coplanares Points Persamaan, contoh dan latihan terselesaikan

Itu Poin Coplanares Mereka semua milik pesawat yang sama. Dua poin selalu coplanares, karena titik -titik ini menentukan garis yang melaluinya Flat Infinites berlalu. Kemudian, kedua titik itu termasuk dalam masing -masing rencana yang melewati garis dan karenanya akan selalu menjadi coplanares.

Di sisi lain, tiga poin menentukan satu bidang, yang diikuti bahwa tiga titik akan selalu menjadi coplanares ke pesawat yang mereka tentukan.

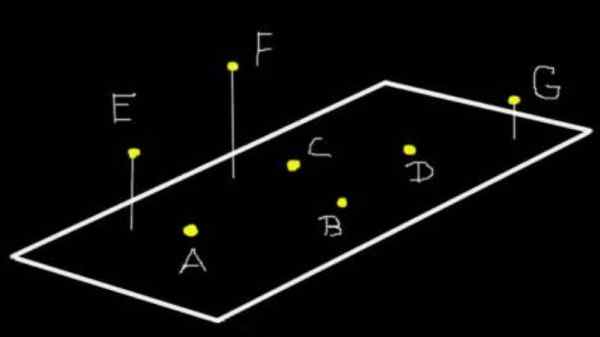
Gambar 1. A, B, C dan D Mereka adalah coplanares ke bidang (Ω). E, f dan g bukan coplanares a (Ω) tetapi jika mereka coplanares ke bidang yang ditentukan tiga. Sumber: f. Zapata.

Lebih dari tiga poin bisa menjadi coplanar atau tidak. Misalnya pada Gambar 1, titik A, B, C dan D adalah coplanares ke bidang (Ω). Tetapi e, f dan g bukan coplanares a (Ω), meskipun mereka adalah coplanares ke bidang yang ditentukan tiga.

[TOC]

Persamaan pesawat yang diberikan tiga poin

Persamaan pesawat yang ditentukan oleh tiga titik yang diketahui a, b, c adalah hubungan matematika yang menjamin bahwa titik p dari koordinat generik (x, y, z) yang memenuhi persamaan milik pesawat tersebut. 

Pernyataan sebelumnya setara dengan mengatakan bahwa jika p dari koordinat (x, y, z) memenuhi persamaan pesawat, maka titik tersebut akan menjadi copatar dengan tiga titik a, b, c yang menentukan pesawat tersebut.

Untuk menemukan persamaan pesawat tersebut, mari kita mulai dengan menemukan vektor AB Dan Ac:

AB = [Bx - kapak, oleh - ay, bz - az]

Ac = [Cx - ax, cy - ay, cz - az]

Produk vektor AB X Ac Ini menghasilkan vektor tegak lurus atau normal ke bidang yang ditentukan oleh titik A, B, C.

Titik koordinat apa pun (x, y, z) milik pesawat jika benar bahwa vektor Ap tegak lurus terhadap vektor AB X Ac, yang dijamin jika dipenuhi:

Dapat melayani Anda: decagon: biasa, tidak teratur, properti, contoh

AP • (AB X AC) = 0

Ini setara dengan mengatakan bahwa produk tiga Ap, AB Dan Ac Menjadi nol. Persamaan sebelumnya dapat ditulis dengan cara matriks:

Contoh

Biarkan poin A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) dan D (ke, 0, 1). Nilai apa yang harus dimiliki ke sehingga keempat poinnya adalah coplanares?

Larutan

Untuk menemukan nilai A, perlu bahwa titik D adalah bagian dari bidang yang ditentukan oleh A, B dan C, yang dijamin jika persamaan pesawat memenuhi.

Mengembangkan penentu yang kami miliki:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2a -8 + 6 = -2a -2 = 0

Persamaan sebelumnya menunjukkan itu A = -1 Untuk memenuhi kesetaraan. Dengan kata lain, satu -satunya cara titik D (ke, 0.1) menjadi coplanar dengan titik A, B dan C adalah itu ke Valga -1. Kalau tidak, itu tidak akan menjadi coplanar.

Latihan terpecahkan

- Latihan 1

Pesawat memotong sumbu kartesius x, y, z masing -masing dalam 1, 2 dan 3. Persimpangan bidang tersebut dengan sumbu menentukan titik A, B dan C. Temukan komponen DZ dari titik D, yang komponen Cartesian yang adalah:

 D (-dz, dz+1, dz) 

Dengan syarat D adalah coplanar dengan titik A, B dan C. 

Larutan

Ketika intersepsi bidang dengan sumbu cartesian diketahui, bentuk segmental dari persamaan bidang dapat digunakan:

x/1 + y/2 + z/3 = 1

Sebagai titik D harus menjadi milik pesawat sebelumnya, Anda harus:

-Dz/1 + (dz + 1)/2 + dz/3 = 1

Artinya:

-Dz + dz/2 + ½ + dz/3 = 1

Dz (-1 + ½ + ⅓) = ½ 

DZ (-1/6⅙) = ½ 

Dz = -3 

Dari yang di atas itu mengikuti titik D (3, -2, -3) adalah untuk berpasangan dengan titik A (1, 0, 0); B (0, 2, 0) dan C (0, 0, 3).

Itu dapat melayani Anda: kriteria kesamaan triangulous

- Latihan 2

Tentukan apakah poin a (0, 5, 3); B (0, 6, 4); C (2, 4, 2) dan D (2, 3, 1) adalah coplanares.

Larutan

Kami membentuk matriks yang pangkatnya adalah koordinat D-A, B-A, dan C-A. Maka penentu dihitung dan diverifikasi apakah nol atau tidak.

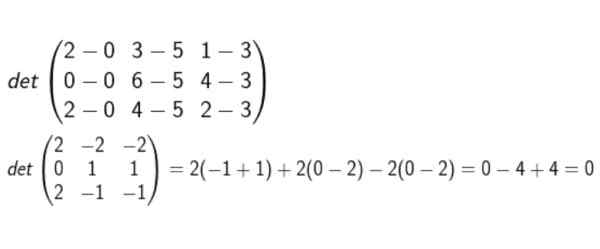
Setelah melakukan semua perhitungan, disimpulkan bahwa mereka adalah coplanares.

- Latihan 3

Dua garis diberikan di luar angkasa. Salah satunya adalah garis (r) yang persamaan parametriknya adalah:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

Dan yang lainnya adalah garis yang persamaannya adalah:

(S): x + 2 y = 1; Z = -1

Menunjukkan bahwa (r) dan (s) mereka lurus coplanarium, yaitu, mereka berada di bidang yang sama.

Larutan

Mari kita mulai secara sewenang -wenang dua poin di garis (r) dan dua di baris:

Lurus (r): λ = 0; A (1, 1, 1) dan λ = 1; B (3, 0, 1)

Mari lakukan x = 0 di telepon=> y = ½; C (0, ½, -1). Dan di sisi lain, jika kita melakukannya y = 0 => x = 1; D (1, 0, -1).

Yaitu, kami telah mengambil poin A dan B yang termasuk dalam garis (R) dan poin C dan D yang termasuk dalam garis (s). Jika titik -titik itu adalah coplanares, maka dua baris juga akan.

Sekarang kami memilih untuk menunjukkan bagaimana pivot dan kemudian kami menemukan koordinat vektor AB, Ac Dan IKLAN. Dengan cara ini Anda mendapatkan:

B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)

C -A: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

D -a: (1-1, 0 -1, -1 -1) => IKLAN= (0, -1, -2)

Langkah selanjutnya adalah membangun dan menghitung penentu yang baris pertama adalah koefisien vektor AB, Baris kedua adalah Ac dan baris ketiga dari vektor IKLAN:

Dapat melayani Anda: Miletus teorema seperti itu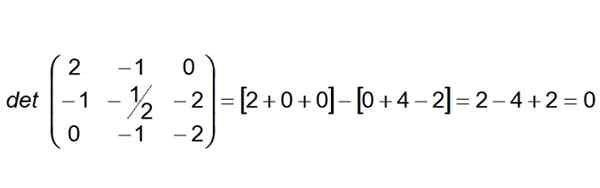

Karena penentu ternyata nol, maka kita dapat menyimpulkan bahwa keempat poinnya adalah coplanarios. Selain itu, dapat dikatakan bahwa garis (r) dan (s) juga coplanares.

- Latihan 4

Garis (r) dan (s) adalah coplanares, seperti yang ditunjukkan dalam Latihan 3. Temukan persamaan bidang yang berisi mereka.

Larutan

Poin A, B, C sepenuhnya mendefinisikan bidang itu, tetapi kami ingin memaksakan bahwa titik x koordinat apa pun (x, y, z) termasuk dalam hal yang sama.

X - a: (x -1, y -1, z - 1) => Kapak= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)

C -A: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

Sehingga x milik bidang yang ditentukan oleh A, B, C dan di mana garis (r) dan (s) terkandung, perlu bahwa penentu yang terbentuk pada baris pertama dibatalkan oleh komponen -komponen dari Kapak, yang kedua oleh orang -orang AB Dan di ketiga oleh orang -orang Ac:

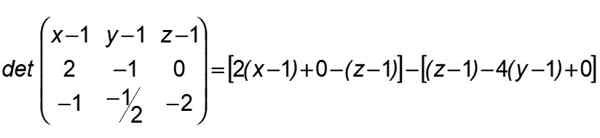
Mengikuti hasil ini, kami mengelompokkan dengan cara ini:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

Dan segera terlihat bahwa itu dapat ditulis ulang seperti ini:

x - 1 + 2y - 2 - z + 1 = 0

Oleh karena itu x + 2y - z = 2 adalah persamaan bidang yang berisi garis (r) dan (s).

Referensi

1. Fleming, w. 1989. Matematika Prealculus. Prentice Hall Ptr.
2. Kolman, b. 2006. Aljabar linier. Pendidikan Pearson.
3. Loyal, J. M. 2005. Geometri analitik datar. Mérida - Venezuela: Editorial Venezuela C. KE.
4. Navarro, Rocio. Vektor. Dipulihkan dari: Buku.Google.bersama.pergi.
5. Pérez, c. D. 2006. Prekalkulasi. Pendidikan Pearson.
6. Prenowitz, w. 2012. Konsep dasar geometri. Rowman & Littlefield.
7. Sullivan, m. 1997. Prekalkulasi. Pendidikan Pearson.