Musim panas teleskopik bagaimana itu diselesaikan dan diselesaikan latihan

Itu penjumlahan Teleskopis Ini adalah cabang operasi dengan seri numerik. Membahas ringkasan elemen dari nilai awal ke “n” ekspresi yang argumennya disebabkan oleh salah satu pola berikut:

(F_X - F_x+1); F_x+1  - F_X)

Di mana ekspresi ringkasannya didefinisikan sebagai berikut: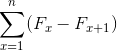

Demikian juga:

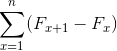
Sumber: Pixabay.com

Mereka mewakili sejumlah elemen yang, ketika berkembang, tunduk pada pembatalan istilah yang berlawanan. Menyebabkan kesetaraan berikut untuk penjumlahan teleskopik:

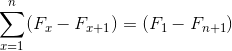
Namanya berasal dari hubungan dengan penampilan teleskop klasik, yang dapat dilipat dan dikerahkan, secara signifikan mengubah dimensinya. Demikian pula, penjumlahan teleskopik, yang dalam sifatnya tidak terbatas, dapat dirangkum dalam ekspresi yang disederhanakan:

F₁ - F_N+1

[TOC]

Demonstrasi

Saat mengembangkan jumlah istilah, penghapusan faktor cukup jelas. Di mana untuk masing -masing kasus, elemen yang berlawanan akan muncul dalam iterasi berikut.

Kasus pertama akan diambil sebagai contoh, (f_X - F_x+1), karena prosesnya bekerja homolog ke (f_x+1-F_X).

Mengembangkan 3 nilai pertama 1, 2, 3 Kecenderungan penyederhanaan diamati

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Dimana dengan mengekspresikan jumlah elemen yang dijelaskan:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Diamati bahwa istilah f₂ dan f₃ Mereka digambarkan dengan lawan mereka, yang membuat penyederhanaan mereka tak terhindarkan. Dengan cara yang sama diamati bahwa istilah f₁ dan f₄ tetap.

Jika jumlahnya dibuat dari x = 1 hingga x = 3, itu berarti elemen itu f₄ sesuai dengan istilah generik f_N+1.

Dengan demikian menunjukkan kesetaraan:

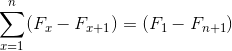
Bagaimana itu terpecahkan?

Tujuan dari penjumlahan teleskopik adalah untuk memfasilitasi pekerjaan, sehingga tidak perlu mengembangkan jumlah istilah yang tak terbatas, atau menyederhanakan beberapa rantai yang terlalu panjang.

Dapat melayani Anda: Metode Trachtenberg: Apa itu, contoh

Untuk resolusi hanya perlu untuk mengevaluasi ketentuan f₁ dan f_N+1. Substitusi sederhana ini merupakan hasil akhir dari jumlah tersebut.

Totalitas istilah tidak akan dinyatakan, menjadi perlu untuk demonstrasi hasil, tetapi tidak untuk proses perhitungan normal.

Yang penting adalah memperhatikan konvergensi dari seri numerik. Terkadang argumen jumlah tidak akan diungkapkan dengan cara teleskopik. Dalam kasus ini, implementasi metode faktorisasi alternatif sangat umum.

Metode faktorisasi karakteristik dalam ringkasan teleskopik adalah fraksi sederhana. Ini terjadi ketika fraksi asli terurai menjadi jumlah beberapa fraksi, di mana pola teleskopik dapat diamati (f_X - F_x+1) atau (f_x+1  - F_X).

Dekomposisi dalam pecahan sederhana

Untuk memverifikasi konvergensi seri numerik, sangat umum untuk mengubah ekspresi rasional dengan metode fraksi sederhana. Tujuannya adalah untuk memodelkan argumen sampai bentuk penjumlahan teleskopik.

Misalnya, kesetaraan berikut mewakili dekomposisi dalam fraksi sederhana:

Saat mengembangkan seri numerik dan menerapkan sifat yang sesuai dengan ekspresi yang diambil sebagai berikut:

Di mana bentuk teleskopik dapat dilihat (f_X - F_x+1).

Prosedur ini cukup intuitif dan terdiri dalam menemukan nilai -nilai pembilang yang, tanpa melanggar kesetaraan, memungkinkan memisahkan produk yang ada di penyebutnya. Persamaan yang muncul dalam penentuan nilai -nilai ini, dinaikkan sesuai dengan perbandingan antara kedua sisi kesetaraan.

Prosedur ini diamati langkah demi langkah dalam pengembangan Latihan 2.

Dapat melayani Anda: 6 teka -teki matematika yang menyenangkan untuk anak -anak

Sejarah

Cukup tidak pasti untuk dapat mendefinisikan momen historis di mana penjumlahan teleskopik disajikan. Namun, implementasinya mulai terlihat pada abad ketujuh belas, dalam studi seri numerik yang dilakukan oleh Leibniz dan Huygens.

Kedua ahli matematika, saat mengeksplorasi penjumlahan dari angka segitiga, mulailah memperhatikan tren dalam konvergensi serangkaian elemen berturut -turut tertentu. Tetapi yang lebih menarik adalah awal pemodelan ekspresi ini, dalam elemen yang tidak perlu terjadi.

Bahkan, ekspresi yang sebelumnya digunakan untuk merujuk pada fraksi sederhana:

Itu disajikan oleh Huygens dan segera memanggil perhatian Leibniz. Siapa yang bisa mengamati konvergensi untuk menilai 2. Tanpa menyadarinya, itu menerapkan penjumlahan teleskopik.

Latihan

Latihan 1

Tentukan istilah mana jumlah berikut menyatu:

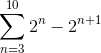
Ketika jumlah dikembangkan secara manual, pola berikut diamati:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶) ... (2¹⁰ - 2^sebelas)

Dimana faktor dari 2⁴ sampai 2¹⁰ Mereka menghadirkan bagian -bagian positif dan negatif, membuat pembatalannya jelas. Maka satu -satunya faktor yang tidak akan disederhanakan adalah yang pertama “2³"Dan yang terakhir" 2^sebelas".

Dengan cara ini, dalam menerapkan kriteria ringkasan teleskopik, diperoleh:

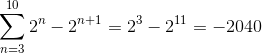
Latihan 2

Ubah argumen menjadi jumlah tipe teleskopik dan tentukan konvergensi seri:

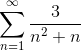
Seperti yang ditunjukkan dalam pernyataan itu, hal pertama adalah terurai dalam fraksi sederhana, untuk memikirkan kembali argumen dan mengekspresikannya dalam bentuk teleskopik.

2 Fraksi yang penyebutnya masing -masing adalah "n" dan "n+1" harus ditemukan, di mana metode yang digunakan di bawah ini harus mencapai nilai -nilai pembilang yang memenuhi kesetaraan.

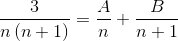
Nilai A dan B didefinisikan. Jumlah fraksi pertama dibuat.

Dapat melayani Anda: 60 pembagi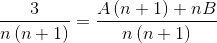

Kemudian, penyebut disederhanakan dan persamaan linier ditetapkan.

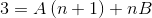
Pada langkah berikutnya ekspresi kanan dioperasikan, sampai pola yang sebanding dengan "3" di sebelah kiri.

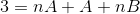
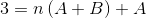
Untuk mendefinisikan persamaan yang akan digunakan, hasil kedua sisi kesetaraan harus dibandingkan. Artinya, tidak ada nilai n variabel yang diamati di sisi kiri, dengan cara ini A +B harus sama dengan nol.

A + b = 0; A = -B

Di sisi lain, nilai konstan harus sama dengan nilai konstan 3.

A = 3

Karena itu.

A = 3 dan b = -3

Sudah mendefinisikan nilai -nilai pembilang untuk fraksi sederhana, jumlahnya sedang memikirkan kembali.

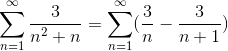
Di mana bentuk generik penjumlahan teleskopik telah tercapai. Serial teleskopik dikembangkan.

Di mana dengan membagi dengan jumlah yang sangat besar hasilnya akan semakin mendekati, mengamati konvergensi seri ke nilai 3.

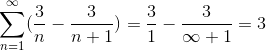
Jenis seri ini tidak dapat diselesaikan dengan kata lain, karena jumlah iterasi yang tak terbatas yang menentukan masalah. Namun, metode ini, bersama dengan banyak orang lain membingkai cabang studi dari seri numerik, yang tujuannya adalah untuk menentukan nilai konvergensi atau menentukan perbedaan seri ini.

Referensi

1. Pelajaran Perhitungan Infinitesimal. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Editum, 1994.
2. Perhitungan Komprehensif: Suksesi dan Serangkaian Fungsi. Antonio Rivera Figueroa. Grup Editorial Patria, 21 Okt. 2014.
3. Kursus dalam Kalkulus dan Analisis Nyata. Sudhir r. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 Jun. 2006.
4. Seri tak terbatas. Benteng Tomlinson. The Clarendon Press, 1930.
5. Elemen teori prosesi tak terbatas. Lloyd Leroy Smail. Perusahaan Buku McGraw-Hill, Incorpan, 1923.