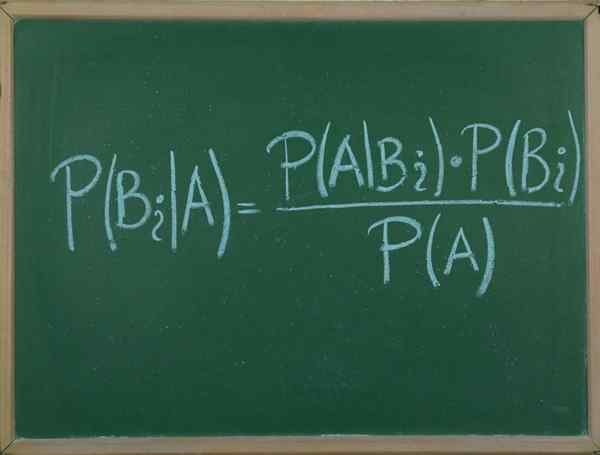Teorema Bayes
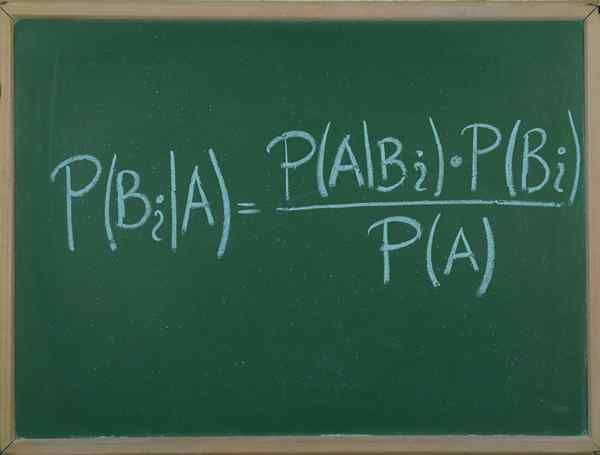
- 4744
- 1286
- Joseph Nader PhD
Kami menjelaskan apa itu teorema Bayes, aplikasinya dan kami menyelesaikan latihan
Apa teorema Bayes?
Dia Teorema Bayes Ini adalah prosedur yang memungkinkan kita untuk mengekspresikan probabilitas bersyarat dari peristiwa acak A dadu B, dalam hal distribusi probabilitas peristiwa B yang diberikan dan distribusi probabilitas hanya untuk.
Teorema ini sangat berguna, karena berkat itu kita dapat menghubungkan probabilitas bahwa suatu peristiwa A terjadi mengetahui bahwa B sedang terjadi, dengan probabilitas bahwa kebalikannya terjadi, yaitu, yang terjadi pada.
Teorema Bayes adalah proposisi perak oleh Pendeta Thomas Bayes, seorang teolog Inggris abad ke -18 yang juga seorang ahli matematika. Dia adalah penulis beberapa pekerjaan dalam teologi, tetapi saat ini dia dikenal karena beberapa perjanjian matematika, di antaranya teorema Bayes yang telah disebutkan sebagai hasil utama.
Bayes berurusan dengan teorema ini dalam sebuah karya berjudul "Esai untuk memecahkan masalah dalam doktrin peluang" (esai untuk memecahkan masalah dalam doktrin kemungkinan), diterbitkan pada 1763, dan di mana besar telah mengembangkan studi dengan aplikasi dengan aplikasi) Di berbagai bidang pengetahuan.
Penjelasan
Pertama, untuk kompresi yang lebih besar dari teorema ini, beberapa gagasan dasar tentang teori probabilitas diperlukan, terutama teorema multiplikasi untuk probabilitas bersyarat, yang menetapkan itu
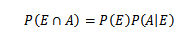
Untuk E dan ke peristiwa sewenang -wenang dari ruang sampel s.
Dan definisi partisi, yang memberi tahu kita bahwa kita memiliki1 ,KE2,… , KEN peristiwa ruang sampel, ini akan membentuk partisi S, jika ayo Mereka saling eksklusif dan persatuan mereka.
Dapat melayani Anda: berapa angka? 8 Penggunaan UtamaMemiliki ini, baik itu acara lain. Jadi kita bisa melihat B sebagai
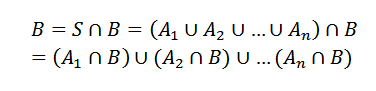
Dimanayo Berpotongan dengan B adalah acara yang saling eksklusif.
Dan sebagai akibatnya,
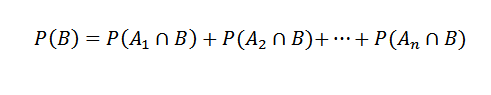
Kemudian, menerapkan teorema multiplikasi
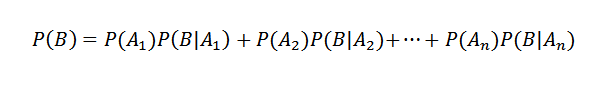
Di sisi lain, probabilitas bersyarat AI B didefinisikan oleh
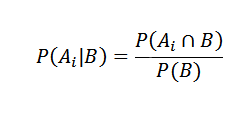
Mengganti dengan benar kami memilikinya untuk saya
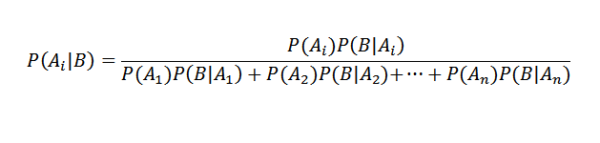
Aplikasi Teorema Bayes
Berkat hasil ini, kelompok penelitian dan beragam perusahaan telah berhasil meningkatkan sistem yang didasarkan pada pengetahuan.
Studi penyakit
Sebagai contoh, dalam studi penyakit, teorema Bayes dapat membantu membedakan probabilitas bahwa suatu penyakit akan ditemukan pada sekelompok orang dengan karakteristik yang diberikan, mengambil data tingkat global penyakit dan dominasi karakteristik tersebut dalam keduanya orang sehat dan sakit.
Pengembangan perangkat lunak
Di sisi lain, di dunia teknologi tinggi, telah mempengaruhi perusahaan besar yang telah berkembang, berkat hasil ini, perangkat lunak "berdasarkan pengetahuan".
Sebagai contoh harian, kami memiliki asisten Microsoft Office. Teorema Bayes membantu perangkat lunak untuk mengevaluasi masalah yang disajikan pengguna dan menentukan saran apa yang akan diberikan dan dengan demikian dapat menawarkan layanan yang lebih baik sesuai dengan kebiasaan pengguna.
Perlu dicatat bahwa formula ini diabaikan sampai akhir -akhir ini, ini terutama karena ketika hasil ini dikembangkan 200 tahun yang lalu, ada sedikit penggunaan praktis untuk mereka. Namun, di zaman kita, berkat kemajuan teknologi yang hebat, para ilmuwan telah mencapai cara untuk mempraktikkan hasil ini.
Latihan terpecahkan
Latihan 1
Perusahaan ponsel memiliki dua mesin A dan B. 54% ponsel dibuat oleh mesin A dan sisanya dengan mesin b. Tidak semua ponsel dalam kondisi baik.
Dapat melayani Anda: faktorisasiProporsi ponsel yang rusak yang dibuat oleh A adalah 0.2 dan untuk B adalah 0.5. Berapa probabilitas bahwa ponsel dari pabrik tersebut rusak? Berapa probabilitas bahwa, mengetahui bahwa ponsel itu rusak, berasal dari mesin untuk?
Larutan
Di sini, Anda memiliki percobaan yang dilakukan dalam dua bagian; Pada bagian pertama peristiwa itu terjadi:
Ke: ponsel yang dibuat oleh mesin a.
B: Ponsel yang dibuat oleh mesin B.
Karena mesin A menghasilkan 54% ponsel dan sisanya diproduksi oleh mesin B, mesin B harus menghasilkan 46% ponsel. Kemungkinan acara ini diberikan, yaitu:
P (a) = 0,54.
P (b) = 0,46.
Peristiwa bagian kedua dari percobaan adalah:
D: Ponsel yang rusak.
E: Sel Non -Defektif.
Seperti yang dinyatakan dalam pernyataan, probabilitas peristiwa ini tergantung pada hasil yang diperoleh pada bagian pertama:
P (d | a) = 0.2.
P (d | b) = 0,5.
Dengan menggunakan nilai -nilai ini, Anda juga dapat menentukan probabilitas aksesori dari peristiwa ini, yaitu:
P (e | a) = 1 - p (d | a)
= 1 - 0.2
= 0,8
Dan
P (e | b) = 1 - p (d | b)
= 1 - 0,5
= 0,5.
Sekarang, acara D dapat ditulis sebagai berikut:
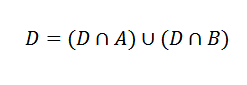 Acara ini saling eksklusif.
Acara ini saling eksklusif.
Menggunakan teorema multiplikasi untuk probabilitas bersyarat adalah:
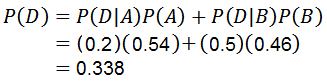
Dengan mana pertanyaan pertama dijawab.
Sekarang kita hanya perlu menghitung p (a | d), untuk teorema Bayes yang diterapkan:
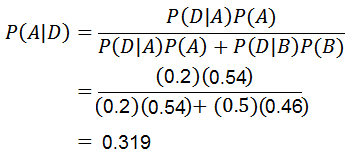
Berkat teorema Bayes, dapat ditegaskan bahwa probabilitas bahwa ponsel telah dibuat oleh mesin A, mengetahui bahwa ponselnya rusak, adalah 0.319.
Dapat melayani Anda: icosagonoLatihan 2
Tiga kotak berisi bola hitam dan hitam. Komposisi masing -masing adalah sebagai berikut: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
Salah satu kotak yang dipilih secara acak dan bola acak diekstraksi darinya yang ternyata putih. Apa yang paling mungkin dipilih kotak?
Larutan
Melalui U1, U2 dan U3, kami juga akan mewakili kotak yang dipilih.
Peristiwa ini merupakan partisi S dan diverifikasi bahwa p (u1) = p (u2) = p (u3) = 1/3 karena pilihan kotak itu acak.
Jika b = bola yang diekstraksi adalah putih, kami akan memiliki p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
Yang ingin kami peroleh adalah probabilitas bahwa bola telah diambil dari kotak IU mengetahui bahwa bola ini putih, yaitu, p (ui | b), dan melihat mana dari tiga nilai yang tertinggi untuk mengetahui yang mana dari kotak mana lebih mungkin untuk ekstraksi bola putih.
Menerapkan teorema Bayes ke yang pertama dari kotak:
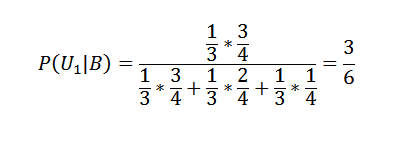
Dan untuk dua lainnya:
P (u2 | b) = 2/6 dan p (u3 | b) = 1/6.
Kemudian, yang pertama dari kotak adalah yang memiliki probabilitas yang lebih besar telah dipilih untuk ekstraksi bola putih.