Definisi Kecepatan Instan, Formula, Perhitungan dan Latihan

Itu Kecepatan seketika Itu didefinisikan sebagai perubahan instan perpindahan dari waktu ke waktu. Ini adalah konsep yang menambah ketepatan studi tentang gerakan. Dan itu adalah kemajuan sehubungan dengan kecepatan rata -rata, yang informasinya sangat umum.

Untuk mendapatkan kecepatan instan, mari kita lihat interval waktu sekecil mungkin. Kalkulus diferensial adalah alat yang sempurna untuk mengekspresikan ide ini secara matematis.

Kecepatan seketika akun untuk kecepatan seluler di setiap titik rutenya. Sumber: Pixabay.

Titik awalnya adalah kecepatan rata -rata:

Sekarang mari kita buat pendekatan Δt ke 0 segala sesuatu yang bisa. Ini adalah batas dan hasilnya akan tepatnya kecepatan instan:

Batas ini diketahui dengan nama turunan. Dalam notasi kalkulus diferensial yang Anda miliki:

Dengan ketentuan bahwa gerakan ini terbatas pada garis lurus, itu dapat dikeluarkan dengan notasi vektor.

[TOC]

Perhitungan Kecepatan Instan: Interpretasi Geometris

Gambar berikut menunjukkan interpretasi geometris dari konsep turunan: itu adalah kemiringan garis garis singgung Ke kurva x (t) vs. T Di setiap titik.

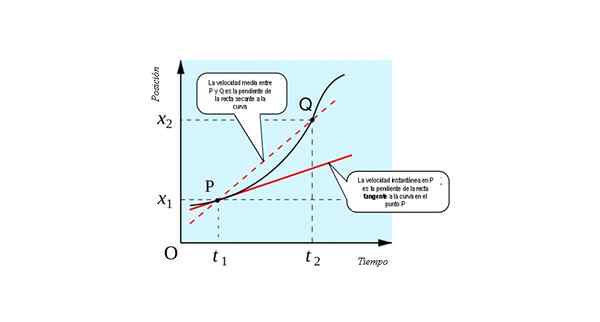Kecepatan sesaat dalam P setara secara numerik ke kemiringan garis garis singgung ke kurva x vs. t pada titik p. Sumber: Sumber: すじにく シチュー [CC0].

Anda dapat membayangkan cara mendapatkan batas jika titik Q secara bertahap mendekat. Akan tiba saatnya kedua titik sangat dekat, sehingga satu tidak dapat dibedakan dari yang lain.

Garis yang menyatukannya kemudian akan mengering (lurus yang memotong menjadi dua titik) menjadi singgung (lurus yang menyentuh kurva pada satu titik). Oleh karena itu, untuk menemukan kecepatan instan dari partikel seluler yang seharusnya kita miliki:

• Grafik posisi partikel sebagai fungsi waktu. Menemukan kemiringan garis garis singgung ke kurva pada setiap momen waktu, Anda memiliki kecepatan sesaat pada setiap titik yang ditempati oleh partikel.

Dapat melayani Anda: hukum ampère: formula dan persamaan, demonstrasi, latihan

O Nah:

• Fungsi posisi partikel x (t), yang diturunkan untuk mendapatkan fungsi kecepatan V (t), Kemudian fungsi ini dievaluasi setiap saat T, Kenyamanan. Fungsi posisi seharusnya dapat diturunkan.

Beberapa kasus khusus dalam perhitungan kecepatan instan

-Kemiringan garis garis singgung ke kurva di P adalah 0. Lereng nol berarti ponsel dihentikan dan kecepatannya tentu saja 0.

-Kemiringan garis garis singgung ke kurva di P lebih besar dari 0. Kecepatannya positif. Dalam grafik di atas itu berarti bahwa ponsel menjauh dari atau.

-Kemiringan garis garis singgung ke kurva di P kurang dari 0. Kecepatannya akan negatif. Dalam grafik di atas tidak ada titik seperti itu, tetapi dalam hal ini partikel akan mendekat atau.

-Kemiringan garis garis singgung ke kurva konstan di P dan semua titik lainnya. Dalam hal ini grafiknya adalah garis lurus dan seluler memiliki Gerakan Garis Seragam MRU (Kecepatannya konstan).

Secara umum, fungsinya V (t) Ini juga fungsi waktu, yang pada gilirannya dapat diturunkan. Bagaimana jika tidak mungkin menemukan yang berasal dari fungsi x (t) Dan V (t)?

Dalam kasus x (t) Bisa jadi kemiringan - kecepatan sesaat - mengubah tanda -tanda tajam. Atau itu akan langsung beralih dari nol ke nilai yang berbeda.

Jika demikian grafiknya x (t) Itu akan menghadirkan tips atau sudut pada perubahan yang tiba -tiba. Sangat berbeda dari kasus yang direpresentasikan pada gambar sebelumnya, di mana kurva x (t) Ini adalah kurva lunak, tanpa titik, sudut, diskontinuitas atau perubahan mendadak.

Dapat melayani Anda: bose einstein kondensat

Yang benar adalah bahwa untuk ponsel nyata, kurva lunak adalah yang paling mewakili perilaku objek.

Gerakan umumnya cukup rumit. Ponsel dapat dihentikan sebentar, percepatan untuk bergerak dari istirahat untuk memiliki kecepatan dan menjauh dari titik awal, menjaga kecepatan untuk sementara waktu, lalu berhenti untuk berhenti lagi dan dengan demikian gayanya.

Mereka dapat memulai lagi dan melanjutkan ke arah yang sama. Atau bertindak kemunduran dan kembali. Ini disebut gerakan yang bervariasi dalam dimensi.

Di bawah beberapa contoh perhitungan kecepatan instan akan mengklarifikasi penggunaan definisi yang diberikan:

Latihan kecepatan seketika terpecahkan

Latihan 1

Sebuah partikel bergerak di sepanjang garis lurus dengan hukum gerakan berikut:

x (t) = -t³ + 2 t² + 6 t - 10

Semua unit berada dalam sistem internasional. Menemukan:

a) posisi partikel pada t = 3 detik.

b) kecepatan rata -rata dalam interval antara t = 0 s dan t = 3 detik.

c) kecepatan rata -rata dalam interval antara t = 0 s dan t = 3 detik.

d) Kecepatan instan partikel dari pertanyaan sebelumnya, pada t = 1 detik.

Jawaban

a) Untuk menemukan posisi partikel, hukum gerakan (fungsi posisi) pada t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Tidak ada masalah bahwa posisinya negatif. Tanda (-) menunjukkan bahwa partikel berada di sebelah kiri asal atau.

b) Dalam perhitungan kecepatan rata -rata, posisi akhir dan awal partikel diperlukan pada waktu yang ditunjukkan: x (3) dan x (0). Posisi pada t = 3 adalah x (3) dan diketahui tentang hasil sebelumnya. Posisi pada t = 0 detik adalah x (0) = -10 m.

Dapat melayani Anda: statis: sejarah, studi apa, aplikasi, hukum

Karena posisi akhir sama dengan yang awal, segera disimpulkan bahwa kecepatan rata -rata adalah 0.

c) kecepatan rata -rata adalah alasan antara jarak yang ditempuh dan waktu yang dihabiskan. Sekarang, jaraknya adalah modul atau besarnya perpindahan, oleh karena itu:

Jarak = | x2 - x1 | = | -10-(-10) | M = 20 m

Perhatikan bahwa jarak yang ditempuh selalu positif.

v_{m = 20 m/3 s = 6.7 m/s}

d) Di sini perlu menemukan turunan pertama dari posisi mengenai waktu. Kemudian dievaluasi untuk t = 1 detik.

x '(t) = -4 t² + 4 t + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Latihan 2

Di bawah ini adalah grafik posisi ponsel sebagai fungsi waktu. Temukan kecepatan instan pada t = 2 detik.

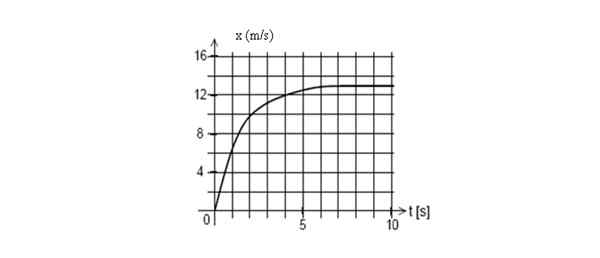Posisi grafik versus waktu untuk ponsel. Sumber: Made sendiri.

Menjawab

Gambar garis singgung ke kurva pada t = 2 detik, lalu hitung kemiringan Anda, mengambil dua titik garis.

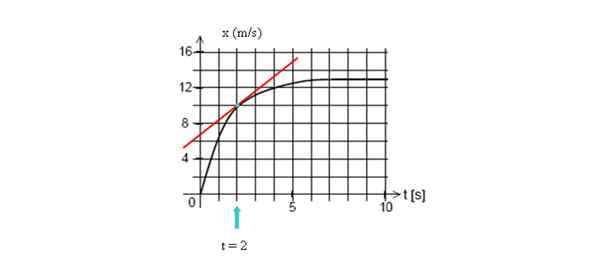Untuk menghitung kecepatan sesaat pada titik yang ditunjukkan, gambar garis singgung ke titik itu dan temukan kemiringannya. Sumber: Made sendiri.

Dalam contoh ini kita akan mengambil dua titik yang mudah divisualisasikan, yang koordinatnya adalah (2 detik, 10 m) dan potongan dengan sumbu vertikal (0 s, 7 m):

Referensi

1. Giancoli, d. Fisika. Prinsip dengan aplikasi. 6^th Edisi. Prentice Hall. 22-25.
2. Resnick, r. (1999). Fisik. Volume 1. Edisi ketiga dalam bahasa Spanyol. Meksiko. Perusahaan Editorial Kontinental S.KE. dari c.V. 21-22.
3. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7^ma. Edisi. Meksiko. Editor Pembelajaran Cengage. 23-25.